A resposta à questão colocada no título foi dada por Isaac Newton, aliás ele foi mais longe. Não só explicou porquê que a Lua não caía na Terra, como também conseguiu compreender porquê que as leis de Kepler (sobre as órbitas dos planetas) eram verdade, porquê que os planetas andam à volta do Sol e em simultâneo, com a mesma teoria, expôs a forma como tudo caía na Terra, (em particular a maçã que alegadamente lhe caiu na cabeça)! Parece quase um paradoxo pensar que com a mesma explicação se consegue dizer porquê que as maçãs caem, mas não a Lua. Esta explicação está presente, claro, na Lei da Atracção Universal, ou se preferirem: Lei da Gravitação Universal, pensada por Newton.
Nesta exposição, porém, não vou explicar detalhadamente essa lei, irei apenas focar-me nos elementos importantes que me conduzam à resposta da questão antes colocada.

Isaac Newton (1643-1727). Provavelmente o Físico mais importante de sempre.
Um ano antes de Newton nascer, morreu Galileu Galilei, aquele que descobriu que toda e qualquer trajectória de um objecto lançado ao ar descreve uma parábola (trata-se de um tipo de curva específica). É algo que todos podemos comprovar no nosso dia-a-dia: se lançarmos uma pedra ao ar (preferencialmente atirando-a para a frente, claro), a pedra acaba sempre por descrever um “caminho aéreo” com um tipo de curvatura parabólico.
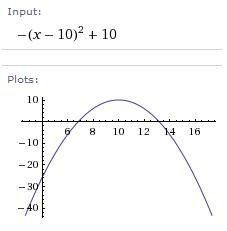
Para quem sabe um pouco de matemática, saberá que uma curva parabólica é descrita por uma função quadrática. Por exemplo:
Se atirarem algo em frente, de uma dada altura, o que esperam observar será uma trajectória deste tipo:

O tipo de trajectória é igual ao anterior, claro, apenas com a diferença de que o movimento começa no ponto mais alto.
Tendo isto em mente, partamos para um dos pensamentos brilhantes de Newton: o conhecido “Canhão de Newton”. Imaginem que constroem uma torre muito alta, e no topo desta colocam um canhão. Se a torre fosse suficientemente alta para estar fora da atmosfera terrestre (na realidade, do ponto de vista de engenharia, tal empreendimento seria praticamente impossível), os projécteis disparados não sofreriam resistência do ar. Se o canhão fosse suficientemente potente, podem começar a imaginar as trajectórias dos projécteis a poderem-se desenhar em relação ao planeta Terra como um todo, ou seja, num referencial que é aproximadamente esférico (e não um plano, como se pode aproximar em situações do dia-a-dia), como podem observar na seguinte figura:
Como podem ver, para uma determinada força de lançamento que o canhão consiga aplicar no projéctil, este poderá sobrevoar toda a Terra e voltar ao ponto de origem, ou seja, de onde foi disparado! Notar um aspecto muito importante: como estamos acima da atmosfera, a resistência ao movimento pode ser considerada nula, logo, se pensarem na lei da conservação da energia, sabem que o projéctil que voltou ao ponto de origem tem a mesma energia do que quando foi disparado, pois se não há resistência, a energia conservou-se, tanto a potencial (porque a altura se manteve constante), como a cinética (em consequência da potencial ter sido constante, bem como a energia total ser necessariamente constante).
Pode-se dizer que nesta situação o projéctil está sempre a cair para a Terra, mas numa direcção que o leva para fora da Terra (a direcção da velocidade nunca aponta em direcção à Terra).
É este o princípio pelo qual se colocam satélites (artificiais) a orbitar a Terra. Claro que nesse caso a analogia sofre uma pequena variação, que é o canhão em vez de estar em cima de uma torre, está simplesmente à superfície da Terra, mas a apontar para cima… (Evidentemente que terá que ser mais “potente” neste caso, para obter o mesmo efeito que o outro era capaz, visto que a força gravítica é maior “cá em baixo” e tem que ser vencida a resistência do ar na descolagem.)
Vídeo do lançamento de um vaivém espacial (Discovery).
A Lua, como sabem, é ela mesma um satélite (natural), que continua em órbita da Terra e assim continuará, devido a este mesmo princípio. A diferença é que no caso da Lua, ela não foi lançada. Está lá devido à forma como se formou (mas isso poderá ser tema para outra discussão). (Na verdade, a Lua está-se a afastar da Terra devido ao efeito de Maré, mas não se preocupem com a hipótese de ficarem sem luar, pois está-se a afastar apenas a uma taxa de 3 cm ao ano.)








1 comentário
3 pings
Graças a Deus
As leis físicas que ele fez, são ótimas!
Afinal quem é Deus? ele pode ser apenas aquele que fez as leis físicas hehe
[…] Como pode então o nosso peso ser zero em queda livre? A nossa massa não varia enquanto caímos, e a gravidade também não (em boa aproximação, veja este artigo). A diferença está no movimento! Quando estão em repouso sobre a balança, a balança exerce sobre vós uma força igual ao vosso peso (terceira Lei de Newton): empurra-vos para cima. Considerem agora que estão num elevador: quando o elevador sobe, ele tem que exercer sobre vós uma força (nos vossos pés) para vos levar para cima com ele. (De forma semelhante, quando aceleram o vosso carro na autoestrada, sentem o vosso corpo a ser “empurrado” para trás.) Isto significa que se levarem a vossa balança para o elevador, e se se colocarem em cima dela, vão ver que o vosso peso aumenta quando o elevador começa a subir. (Há vários problemas com esta experiência, a começar pelo facto de a maioria das balanças ter um tempo de resposta bastante lento, pelo que o que vocês iriam ver era o peso a mudar, mas provavelmente não conseguiriam fazer uma leitura clara dos números. Notem que mesmo que fizessem a experiência num prédio com muitos andares, isso não garantia resultados mais animadores, porque o que conta é a aceleração do elevador. Quando este se move a velocidade constante, o vosso peso volta ao “normal”. Tal como na autoestrada, quando o carro atinge uma velocidade constante, deixamos de nos sentir empurrados contra o banco.) Por outro lado, para o elevador parar, tem que desacelerar: isto faz com que o vosso peso diminua. De igual modo, quando o elevador começa a descer, o vosso peso diminui. Se o cabo do elevador se partir, o elevador cai em “queda livre”, e o vosso peso é zero durante a queda! Porquê? Porque quer o elevador, quer a balança, quer o vosso corpo, sentem todos apenas a força gravítica. Caem em “paralelo” e por isso as forças de contacto são nulas. Podem recordar a suposta experiência do Galileu na Torre de Pisa (alegadamente inventada pelo seu biógrafo): se tudo cai com a mesma aceleração, então dois objectos que caiam da mesma posição com a mesma velocidade, deverão cair sempre paralelamente (com igual velocidade, ainda que esta não seja uma constante). Naturalmente, no momento do embate a aceleração é contrária à gravidade, e por isso o vosso peso aumenta muito, podendo ter as consequências que imaginam. Em contraste, os astronautas que estão dentro da estação espacial, em condições de “gravidade zero”, a “flutuar”, não têm este problema, porque nunca chegam a sofrer a colisão. (Recordemos que um objecto em órbita está sempre a “cair” mas numa direcção que o mantém sempre aproximadamente à mesma distância da Terra; ver o artigo “porque é que a Lua não cai?”). […]
[…] História do Conhecimento. 7 Equações que governam o mundo. Bússola. Balão de Ar Quente. Lei da Gravitação Universal. Holograma. Criptografia. Espaço Vazio. Composição do Corpo […]
[…] Terra orbita o Sol devido à força gravítica que atrai a Terra para o Sol (ver o artigo Porque é que a Lua não cai na Terra? para mais pormenores sobre orbitação), e como é evidente, orbita-a como um “todo”, visto […]