Da Física da Continuidade à Física das Transições de Fase

Normalmente as pessoas pensam que a maior descoberta de Newton foram as leis do movimento e a Lei  da Gravitação Universal. De facto, para ele chegar aí teve que inventar algo ainda mais importante, aquilo que tinha impedido outros antes dele, como Galileu, de alcançar essas leis, a ferramenta matemática para lidar com a Física do movimento: Cálculo (diferencial e integral). O Cálculo foi de extrema importância para o desenvolvimento da física teórica, o que ainda é válido nos progressos que se fazem actualmente em vários ramos da Física!

Newton inventou o Cálculo a uma velocidade impressionante – mais ou menos à mesma velocidade com que os estudantes o aprendem no ensino superior! Poucos anos depois, Leibniz inventou independentemente também o Cálculo, na forma que é hoje usada, por ser bastante mais conveniente que a de Newton, que acabou só por publicar os seus estudos por Leibniz o ter feito também (na verdade, houve grande polémica em torno da questão de quem teria sido o primeiro, sendo até ainda uma das questões mais apaixonantes para os historiadores de ciência, mas a questão ficou resolvida na altura a favor de Newton, visto que a decisão de determinar quem teria sido o primeiro dependia do parecer do presidente da Royal Society, o qual era, “por acaso”, o próprio Newton! Ainda assim, acredita-se actualmente que de facto Newton foi o primeiro.).

Newton ganhou o jogo, porque era ele que definia as regras. Regra número 1: “Eu ganho.”

 Qual a importância do Cálculo na Física?

Um físico teórico tem normalmente o intuito de descrever um fenómeno de modo quantitativo, de tal modo que possa comparar valores numéricos do seu modelo matemático, com valores numéricos que possam ser medidos através de uma experiência. Assim, o físico retrata o seu modelo através de uma, ou mais, equações (igualdade matemática que estipula a relação entre um certo conjunto de variáveis). Exemplo: v=x/t, em que ‘v’ representa velocidade, ‘x’ representa espaço e ‘t’ representa tempo; a equação descreve a determinação da velocidade média que se tem quando se percorre a distância x, no tempo t.

Em Física, está-se muitas vezes interessado em saber como é que as coisas variam ao longo do tempo, porque é isso que define o seu comportamento. Portanto, considerando o exemplo anterior, saber a velocidade média de um movimento está longe de ser uma descrição completa de como variou a velocidade do corpo ao longo do tempo t – convém saber como é que foi a velocidade da partícula em cada instante de tempo, nesse intervalo de tempo t, para se ter uma descrição completa da variável velocidade.

Considere-se o exemplo:

Não sei se o leitor está familiarizado com análise de gráficos, mas é simples: no eixo horizontal (normalmente denominado de eixo das abcissas, ou dos xx) está representada a variação temporal, ou seja, pode-se considerar que zero é quando se começou uma dada experiência, e ao longo do tempo foram-se registando valores da posição x, os quais estão no eixo vertical (normalmente denominado de eixo das ordenadas, ou dos yy). A curva azul resulta da união de todos os dados de uma possível experiência que iria simplesmente consistir em olhar para um temporizador – anotar o tempo, olhar para um medidor de distância – anotar a distância; fazer isto muitas vezes… Colocar todos os pares de valores tempo-distância no gráfico, ligar os pontos aos seus vizinhos mais próximos, e assim surge uma curva (não necessariamente igual à que coloquei no exemplo, claro).

Se o que estive a dizer até agora ofende a inteligência do leitor, peço desculpa. Passemos então a coisas mais interessantes: a recta preta intersecta dois pontos (a vermelho) da curva azul que define a forma como a posição de um dado corpo variou ao longo do tempo (não coloquei indicação sobre as unidades, ou seja, se quiserem podem entender aqueles números como sendo segundos, minutos, horas, etc., no caso do tempo, e metros, quilómetros, anos-luz, etc., no caso da posição x). O declive desta recta, que é definido pelos dois pontos escolhidos, dá-nos a velocidade média que o corpo teve neste período de tempo – isto pode ser compreendido intuitivamente, pois uma recta, neste gráfico, define basicamente que para uma dada variação de tempo, temos sempre a mesma variação da posição (exemplo: do tempo t=30 até t=40, percorreu-se o mesmo espaço que de t=40 até t=50) – o mesmo, não é válido, claro, no caso da curva azul.

Como disse anteriormente, estamos interessados na velocidade instantânea (em cada instante), portanto e pensando como os físicos costumam fazer: a velocidade instantânea é basicamente a situação limite do cálculo da velocidade média durante um período de tempo muito curto. Graficamente, isto significa que se aproximarmos muito os dois pontos vermelhos (através da curva azul), quando eles forem coincidentes, temos a velocidade instantânea. Assim, enquanto a velocidade média é o declive de uma recta concorrente à curva em dois pontos, a velocidade instantânea é o declive da recta tangente a um ponto. Através do raciocínio anterior de aproximar dois pontos, reparamos que o declive da recta tangente é muito próximo do declive de uma recta concorrente a dois pontos muito próximos do ponto desejado. Na verdade, para quem está familiarizado com o conceito de “limite”, perceberá que então a velocidade instantânea calcula-se através de um limite, que é a situação limite de os dois pontos coincidirem. Isto, na verdade, não é mais que o conceito de derivada, que está na base do cálculo diferencial (aqui não vou falar do cálculo integral, mas na verdade, trata-se de fazer o “contrário” da derivada; no exemplo, tendo a equação que explicita a variação da posição com o tempo, pode-se fazer a derivada desta própria equação, obtendo desse modo o perfil de velocidade instantânea para todos os pontos; caso se pretendesse fazer o contrário, ou seja, através da curva de velocidade obter a curva da posição em função do tempo, tal também seria possível, através do cálculo “inverso” à derivada, que é o integral).

O Cálculo serve, então, ao físico, como ferramenta para tratar toda a Física que envolva a variação de uma medida ao longo do tempo. Exemplos:

• Ter um sistema de partículas, onde o volume, a pressão e a temperatura variam ao longo do tempo – será necessário compreender como é que variam, para se ter uma descrição completa do que se está a passar, para se ser capaz, em última instância, de prever o futuro do sistema; ou por outras palavras, de ser capaz de dominar o sistema, de tal modo que possa ter uma aplicação tecnológica.
• Ter um circuito eléctrico, onde a corrente eléctrica, bem como a tensão podem variar ao longo do tempo, nos terminais de um componente – para compreender o funcionamento do componente, é necessário perceber a forma como variam essas grandezas.
• No sistema solar, se se quiser prever como é que vão evoluir as órbitas dos planetas, é necessário determinar as equações diferenciais que governem a variação destas órbitas, tendo em conta todas as variáveis presentes (o que é ainda um problema em aberto, para uma escala temporal que envolva a expansão total do Sol para uma gigante vermelha).

Entre inúmeros outros exemplos que poderia dar.

No quadro – “x+2=5 … x=3”. Aluno: “Espere lá! Ainda ontem tinha ensinado que x era igual a 2!!”

Quer então dizer que Newton inventou a Matemática necessária para descrever tudo o que se passa no universo?

Não. O cálculo diferencial aplica-se necessariamente a “coisas” que variem de modo contínuo, isto é, de um modo perfeitamente “regular”. Ou seja, numa experiência, se estivermos a medir o comportamento de uma dada coisa, digamos a corrente eléctrica de uma amostra ao longo do tempo, esta corrente não pode variar abruptamente, isto é, se estivermos a verificar que em cada minuto, a amostra varia 1mA, não pode acontecer, que haja um minuto em que haja uma variação de 100 A, tendo sido registados 100A (por exemplo), simplesmente porque o aparelho não permitia medir mais! Graficamente, significa que não podemos calcular a derivada de uma descontinuidade – uma variação brusca, ou um “pico”.

É aqui que surge a Física das Transições de Fase, que só foi desenvolvida no século XX, principalmente por Landau (físico russo que ganhou o Prémio Nobel por algumas das suas contribuições).

Lev Landau – ganhou o Prémio Nobel da Física em 1962, pela sua teoria sobre a superfluidez do Hélio líquido II.

O que é isso de uma “transição de fase”?

Considere-se um líquido – a matéria que constitui este líquido comporta-se de forma perfeitamente similar, quer o líquido esteja muito quente, ou muito frio. Contudo, se a temperatura (ou a pressão) variar o suficiente para transformar esse líquido num sólido, ou num gás, aí as coisas variam drasticamente! No caso do sólido, a matéria passa-se a agrupar de modo muito mais ordenado, passando a ter interacções entre si muito mais fortes, e que dão origem a propriedades completamente diferentes do material! Portanto, se estivéssemos a medir uma propriedade eléctrica, por exemplo, do líquido, e este passasse de repente a sólido (através de variação da temperatura, por exemplo), as propriedades eléctricas a serem medidas (como a resistência, por exemplo) poderiam ter uma variação drástica no ponto de distinção entre estas duas fases.

Por outras palavras, o leitor conhece algumas transições de fase: ebulição da água, fusão do gelo, etc.. Um exemplo de descontinuidade numa variável conhecida associada à transição de fase da água, é a da densidade. O gelo flutua, o que significa que o gelo é menos denso que a água. Assim, se estivéssemos a medir a densidade de um pedaço de água, e esta de repente passasse a gelo, a densidade daria um “salto” para um valor totalmente diferente.

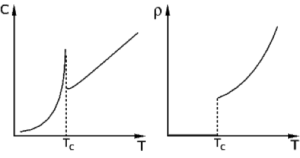
Gráficos típicos no estudo da supercondutividade.  À direita gráfico da resistividade em função da temperatura e à esquerda gráfico do calor específico também em função da temperatura para o mesmo material. Em Tc dá-se uma transição de fase (para T<Tc está-se numa fase supercondutora, enquanto que para T>Tc está-se numa fase “normal”).

As fases que conheço para a matéria são “sólido”, “líquido” e “gasoso”. Se se conhecerem as transições entre cada uma destas fases, a Física das Transições de Fase fica “arrumada”?

Não. Apesar das fases mais conhecidas que a matéria pode tomar sejam efectivamente essas, existem outras. Note-se bem: uma “fase” não denota algo visual ou táctil, que possamos distinguir facilmente, como o caso do sólido, líquido ou gasoso – não é isso que está em causa, mas sim o comportamento da própria matéria. Assim, pode haver uma transição de fase, sem que a matéria altere o seu aspecto visual ou táctil. Um exemplo é a transição de uma fase dita “normal” para uma fase “supercondutora”. A transição de fase não tem que envolver uma variação total de todas as propriedades do material. Por exemplo, tanto a água como o gelo não têm cheiro (o cheiro, obviamente, não é uma propriedade física mensurável, ainda assim dá para perceberem a ideia). No caso da supercondutividade, o metal “normal” que passou a “supercondutor”, não alterou, por exemplo, a sua rigidez (não necessariamente), mas variou de modo drástico as suas propriedades eléctricas (em particular, a resistência terá passado de um valor qualquer, para exactamente zero, na fase supercondutora).

Na verdade, a Física das Transições de Fase é mais geral que isto: não se aplica apenas à matéria! O mesmo tipo de análise pode ser feito para o estudo de muitas outras coisas – à partida, para tudo o que passe de um dado “estado”, para outro “estado”, de modo descontínuo. Por exemplo, recentemente descobriu-se que no cérebro, os neurónios na sua actividade podem transitar entre diferentes estados de “funcionamento” através de transições de fase.