Neste artigo irei falar sobre a razão de ouro, bem como onde esta pode ser encontrada, tentando desmistificar um pouco algumas ideias que se têm vindo a difundir. Quem não sabe, tem a tentação de generalizar para simplificar, o que, em matérias exactas como a Matemática, onde não há espaço para subjectividade, é normalmente um erro. É o que acontece neste caso: como a razão dourada e os números de Fibonacci aparecem em muitas manifestações da natureza, cai-se no erro de forçar o seu aparecimento em muitas outras, onde na verdade não está presente (ou pelo menos não há evidências suficientes para o afirmar). Faço a nota que até muitos matemáticos e arquitectos falham na distinção entre o verdadeiro e o falso neste assunto! E, claro, pela web podem encontrar milhares de páginas a expor os mitos, como se fossem verdade.
Comece-se então pelo princípio: o que é a razão de ouro?
A razão de ouro (número de ouro, proporção áurea, divina proporção, entre outros nomes semelhantes) está associada ao rectângulo de ouro (relembro que razão é o mesmo que divisão ou cociente). Este rectângulo tem a particularidade de ter lados tais que se verifica a seguinte condição:
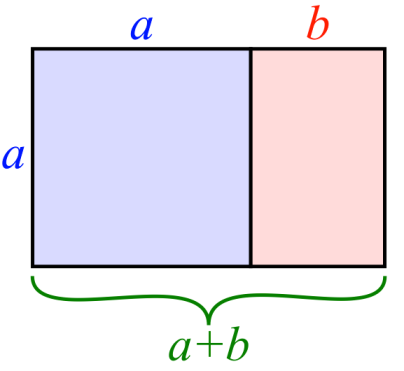
Onde ‘a’ e ‘b’ são dois comprimentos de acordo com a seguinte figura:
A equação de cima significa que o lado maior (a+b) a dividir pelo lado menor (a) do rectângulo é igual ao lado menor (a) a dividir pela diferença entre o lado maior e o lado menor (a+b-a=b). A razão a/b é a razão de ouro, que é convencionalmente denotada pela letra grega φ (a sua definição já vem de Euclides, embora os nomes pomposos só tenham aparecido mais recentemente), cujo valor numérico se pode obter da equação de cima, resolvendo-a:
Nestes cálculos usei a fórmula resolvente para uma equação de segundo grau e desprezei a solução negativa, porque φ é a razão entre dois comprimentos, o que implica que não possa ser negativo. Notem que o último sinal de igualdade é “ondulado”, porque aquele é apenas um valor aproximado, dado que φ é na verdade um número irracional (só representável, portanto, por uma dízima infinita não periódica).
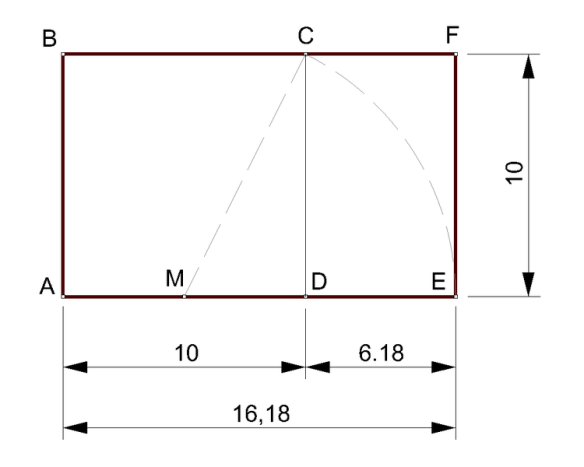
Este rectângulo pode ser desenhado de forma muito simples, precisam apenas de uma régua e de um compasso:
Como a figura sugere, primeiro fazem um quadrado (com os vértices ABCD). De seguida, colocam a agulha do compasso no ponto M (ponto intermédio entre A e D) e desenham o arco que passa pelo ponto C e que “corta” a extensão do segmento de recta AD em E. Uma vez tendo o ponto E, já facilmente “fecham” o rectângulo. Este é um rectângulo de ouro (ABFE). Da primeira equação decorre que o rectângulo CDEF também seja um rectângulo de ouro! Se o leitor tiver um pouco de curiosidade matemática, estará certamente a questionar-se como é que esta construção geométrica conduz à condição antes indicada. Desafio o leitor a chegar à resposta. Caso esta não lhe interesse, pode passar já ao próximo parágrafo, pois irei aqui explicar resumidamente a solução. Primeiro acha-se o comprimento MC, que é a hipotenusa de um triângulo rectângulo, a qual pode ser obtida usando o Teorema de Pitágoras. Em seguida, só têm que constatar que o lado AE é igual à soma de AM com MC, visto que MC é o raio de uma circunferência que passa por C e por E. Ao relacionarem os comprimentos, obtêm a condição anterior. Em linguagem matemática, usando AD=a, DE=b, e MC=x, tem-se que:
Mas o que tem de especial este rectângulo, pergunta o leitor, além de obedecer à tal condição de cima? Porquê “dourado”? O que tem o rectângulo de “divino”?
É aqui que surgem os factos surpreendentes, mas também os mitos de quem queria ver o rectângulo de ouro em todo o lado:
1 – Primeira alegação: o rectângulo dourado tem proporções tais que o sistema cognitivo humano reconhece-o como o rectângulo mais “agradável” e “harmonioso”!
Esta alegação é FALSA! Estudos no âmbito da psicologia refutam este mito, pois, para começar, o nosso julgamento do que é harmonioso ou não depende de muitos outros atributos e circunstâncias. Notem, também, por exemplo, que um rectângulo dourado tem proporções exactas! Se alterarem 1% de um dos lados, o rectângulo já não é dourado, contudo aos vossos olhos poderá parecer que nem sofreu qualquer alteração. Até pode ser que o que consideremos harmonioso seja um rectângulo que em média coincide mais ou menos com um rectângulo dourado, contudo não há evidências suficientes para afirmar isto.
2 – Segunda alegação: o rectângulo de ouro dá-nos uma noção de infinito.
VERDADEIRO! A figura anterior trouxe à luz uma característica interessante: ao construirmos um rectângulo de ouro, aparece-nos um outro. Se pegarem no rectângulo mais pequeno, facilmente criam outro rectângulo dourado mais pequeno dentro dele, ao criarem um quadrado dentro desse rectângulo. Por outras palavras, quando têm um rectângulo dourado de lados ‘a+b’ e ‘a’, ao desenharem o quadrado de lado ‘a’ dentro desse rectângulo, sobra um pequeno rectângulo de lado ‘b’ e ‘a’. Este rectângulo também é dourado, devido à condição inicial. Assim, podem continuar indefinidamente a criar rectângulos de ouro dentro de outros rectângulo de ouro, ao “removerem” o quadrado interior. Naturalmente, o processo inverso também é válido, a partir do qual podem obter rectângulos de ouro cada vez maiores: em vez de removerem um quadrado, neste caso adicionam um quadrado de lado igual ao lado maior do rectângulo de ouro… Assim, o rectângulo de ouro dá-vos uma noção interessante sobre o conceito de infinito, já que através de um, podem construir infinitos rectângulos semelhantes (com a mesma proporção entre os lados).
A proporção divina também pode ser escrita sob a forma de somas infinitas:
A sua demonstração é extremamente simples, basta partirem da equação de segundo grau antes obtida, e fazer um processo iterativo (substituir do lado esquerdo a expressão antes obtida):
E para o outro caso:
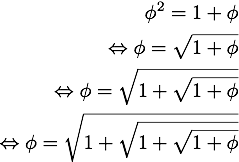 (Nota: mais uma vez, a solução negativa foi desprezada, porque o número de ouro é necessariamente positivo por definição.)
(Nota: mais uma vez, a solução negativa foi desprezada, porque o número de ouro é necessariamente positivo por definição.)
3 – Terceira alegação: é possível encontrar o rectângulo dourado em muitas construções arquitectónicas, desde a antiguidade, até aos tempos modernos!
Na sua grande maioria: FALSO!
Partenon de Atenas:
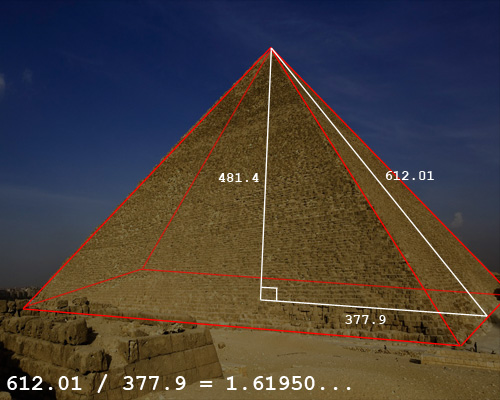
Pirâmides do Egipto:
Catedral de Notre-Dame de Paris:
Edifício das Nações Unidas em Nova Iorque:
Entre muitos outros. Quando os arquitectos são questionados sobre o uso do rectângulo dourado na arquitectura moderna, muitos são os que dizem que realmente é usado, porém são quase sempre os “outros” a usar, pois eles próprios usam apenas proporções semelhantes. Um arquitecto que efectivamente usou deliberadamente a “proporção divina” foi o Le Corbusier, mas é uma clara excepção!
Note-se nas figuras de cima que a colocação dos rectângulos é forçada, sendo que muitos até são colocados em locais pouco “lógicos” (de forma arbitrária). Além disso, as arestas do rectângulo na figura, no tamanho real não são apenas arestas, pois têm espessura!… Ainda assim, não obstante tudo isto, não deixa de ser fascinante que haja em alguns destes casos uma semelhança entre essas construções e o rectângulo dourado. A semelhança pode ser apenas aparente (não sendo por isso matematicamente exacta), mas está lá. E o facto de ter sido por coincidência (visto não haver evidências de que os arquitectos a tenham usado com intenção), é ainda mais interessante!… (De certo modo, pode-se dizer que este mito está mais associado à forma como a ideia é por vezes defendida.)
4 – Quarta alegação: existe uma relação entre o número de ouro e os números de Fibonacci e consequentemente com inúmeros padrões na natureza!
VERDADEIRO! Existe um MAS neste facto: cuidado com os padrões, pois nem todos correspondem a Fibonacci e consequentemente ao número de ouro.
Antes de mais, para quem não sabe, Leonardo de Fibonacci (ou Leonardo de Pisa) foi um matemático italiano que viveu entre os séculos XII e XIII e que é famoso pelos números (ou sequência) baptizados com o seu nome.
A sequência começa com 0 e 1, e os números seguintes são dados pela soma dos dois anteriores. Assim, o terceiro número é 0+1=1, o quarto número é 1+1=2…
Eis os primeiros números da sequência: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
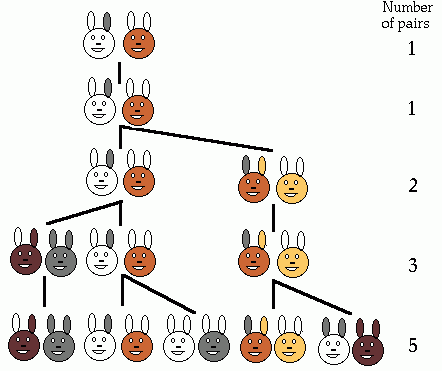
Esta sequência surgiu do estudo que este matemático fez sobre a reprodução de coelhos: no seu modelo, Fibonacci assumiu que os coelhos não morriam, atingiam a maturidade num mês, e se reproduziam de mês a mês, dando à luz sempre um casal. Assim, começando com um par de coelhos, começou a contar os pares de coelhos que ia tendo ao fim de cada mês:
No primeiro mês existe um casal. No segundo mês ainda não se reproduziram, pelo que continua a só haver um casal. No terceiro mês reproduziram-se, pelo que já existem dois casais. No quarto mês o primeiro casal reproduz-se, mas não o segundo, porque ainda não têm dois meses… E assim sucessivamente.
O modelo pode parecer idiota*, por ser muito pouco realista, por outro lado, a sequência dos números parece ser muito simples, sendo quase normal desconfiar que não tem nada de especial. Mas a verdade é que é muito especial! Primeiro, porque a razão entre um número da sequência e o número imediatamente antes (nessa sequência) converge para a razão de ouro, à medida que consideramos números maiores nesta sequência. Em linguagem matemática, usando Fn para denotar o número ‘n’ na sequência de Fibonacci:
![]()
Podem verificar com a calculadora: 1/1= 1, 2/1= 2, 3/2=1.5, 5/3=1.6(6), 8/5 =1.6, etc.. À medida que usam números maiores da sequência, o resultado da divisão é mais próximo do número de ouro (que é o mesmo que dizer que converge). (Obviamente, a demonstração deste resultado não pode ser feito com a calculadora, porque é necessário mostrar para todos os números da sequência, os quais são infinitos. Aqui aparece a vantagem da Matemática analítica sobre a Matemática computacional… Embora a demonstração desta convergência até nem seja difícil, não a incluo aqui para não tornar o artigo demasiado pesado, mas se o leitor tiver interesse, facilmente a encontra noutros sites.)
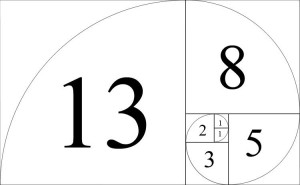
Já vimos que existe realmente uma relação com o número de ouro, falta encontrar então os padrões na natureza. Para isso, convém começar por mostrar mais uma particularidade dos números de Fibonacci: a sua representação geométrica usando quadrados adjacentes cuja área é igual aos números da sequência, como podem ver na imagem seguinte.
Para fazer emergir a espiral basta colocar o compasso centrado no vértice que faz fronteira com os quadrados de área 1 e 2 e desenhar o arco de circunferência que atravessa os quadrados de área 1. Para o quadrado de área 2 já têm que alterar o centro da circunferência (porque o raio já é maior), e o mesmo acontece para os restantes quadrados. Se tiverem uma folha de papel quadriculado e um compasso, poderão facilmente reproduzir a imagem de cima.
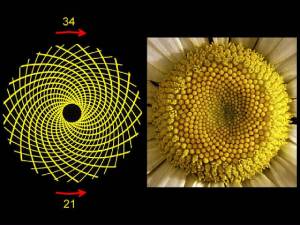
No mundo da natureza podem encontrar muitas vezes os números de Fibonacci e a sua espiral. Por exemplo, o número de pétalas de muitas flores tende a coincidir com estes números. O número de folhas de muitas plantas também. As razões de Fibonacci também aparecem em muitos padrões naturais (5/3, 8/5, …). E claro, também as espirais (normalmente em número igual a um número de Fibonacci):
Em muitos destes casos é possível contar espirais em dois sentidos, sendo que, como na última imagem, no caso de uma pinha, os números de espirais em cada um dos sentidos é diferente, sendo números consecutivos na sequência de Fibonacci (8 e 13 na imagem de cima – o 13 têm que ser vocês a contar, no sentido oposto). Desafio o leitor a tentar encontrar padrões deste género quando tiver oportunidade.
Contudo, como disse, existe um grande MAS! Como seria de esperar, quem não for matemático irá apenas preocupar-se em encontrar novas espirais, sem dar grande importância se essas espirais são efectivamente de Fibonacci, ou não. Como é evidente, existem outras espirais diferentes, com proporções diferentes.
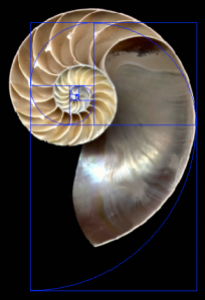
O exemplo mais crítico é o caso da concha Nautilus:
A sua espiral não é uma espiral de Fibonacci, mas sim uma espiral logarítmica (o que significa que se afasta do centro a uma taxa diferente):
A espiral desenhada é a que está relacionada com a proporção divina, que como vêem é diferente!
Outras vezes surgem padrões, números e espirais semelhantes aos de Fibonacci, mas que são diferentes. É o que acontece com os números de Lucas, uma sequência que se constrói do mesmo modo que a de Fibonacci, mas que tem um começo diferente (em vez de ser 0 e 1, como em Fibonacci, começa com 2 e 1), o que implica que toda a sequência tenha números diferentes:
2, 1, 3, 4, 7, 11, 18, 29, 47…
Também neste caso podem construir uma espiral com quadrados, semelhante à de Fibonacci, e, mais importante que isso, também neste caso a razão entre dois números consecutivos se aproxima do número de ouro! O leitor talvez esteja a pensar que provavelmente qualquer sequência de números construída através da regra de o novo número é igual à soma dos dois anteriores, como na sequência de Fibonacci e de Lucas, dará origem à razão de ouro. De facto, assim é! (Se fizerem a tal demonstração, ou a procurarem, irão compreender porquê: o resultado não depende das “condições iniciais”, isto é, dos números com que começam a sequência.)
A questão natural que podem colocar é sobre o porquê de a natureza parecer “gostar” do número de ouro para compor os seus padrões. Não é ao acaso que tal acontece! Em 1993, Douady e Couder chegaram a uma explicação (que não tem que ser única!): no caso das plantas, estas tendem a organizar as suas folhas em espirais de Fibonacci porque essa é a organização que maximiza a exposição das folhas à luz solar. Por outro lado, como vamos ver mais à frente (na parte dos fractais), a razão de ouro está também associada a um maximizar do “empacotamento”, o que também pode ser usado pela natureza para optimizar certos processos biológicos. (A optimização na natureza dá-se em grande parte devido à selecção natural responsável pela evolução: os seres vivos que têm melhor “performance” biológica tendem a sobreviver em maior número que os outros…)
Tem-se ainda que ter cuidado com as espirais forçadas que as pessoas querem ver:

A semelhança em alguns casos até pode existir, mas, como disse, em Matemática (e em Ciência em geral) semelhanças não chegam para se fazerem afirmações deste género.
5 – Quinta alegação: pintores como Leonardo da Vinci e Botticelli terão usado o rectângulo dourado para darem harmonia às suas obras, sendo o mesmo identificável nas suas obras mais conhecidas.
FALSO! As seguintes obras não foram desenhadas com a ajuda do rectângulo dourado, nem faz sentido tentar identificá-lo nelas.
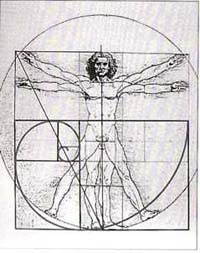
Homem de Vitrúvio de Leonardo da Vinci:
Mona Lisa (A Gioconda) de Leonardo da Vinci:
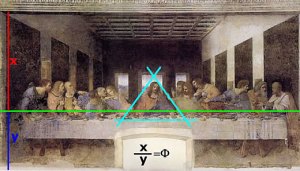
A Última Ceia de Leonardo da Vinci:
O Nascimento de Vénus de Sandro Botticelli:

Todas estas linhas são forçadas por quem quer ver aquilo que julga lá estar. Basta olhar com espírito crítico para as linhas e facilmente se questiona o porquê de as mesmas começarem num sítio e não noutro. Não existe nenhuma boa razão para crer que estes (e outros) artistas tenham usado a razão dourada nos seus desenhos e pinturas! Leonardo da Vinci é evidentemente aquele que é mais vezes citado porque era amigo de Luca Pacioli (matemático italiano), o qual lhe terá falado da “razão divina” (este termo foi na verdade inventado por este matemático!). (Não confundir este matemático com o Édouard Lucas, o “criador” da sequência antes referida, matemático francês que viveu no século XIX e que também é conhecido pelo jogo “Torre de Hanoi”, que o leitor talvez conheça – se não, desafio-o a pesquisá-lo e a jogá-lo).
Contudo, existem efectivamente alguns artistas que exploraram e estudaram a razão dourada nos seus trabalhos, ainda que raramente a tenham realmente usado nas obras finais. Um exemplo é Salvador Dali.
Também na música se tem tentado encontrar o número de ouro, em compositores como Mozart e Bartok, porém, nestes casos, é FALSO! Talvez Debussy tenha usado, não se sabe bem, mas é uma clara excepção!
Também em vários escritos se tenta reconhecer o número de ouro, em particular na Bíblia, não havendo, porém, razões para acreditar nisso. (Existem alguns poetas que usaram uma métrica deliberadamente coincidente com os números de Fibonacci, mas são raridades.)
Mais uma vez faço a ressalva apontada antes: por vezes existem padrões em obras artísticas que de algum modo se aproximam da razão de ouro! Este é de certo um facto fascinante, mas que deve ser analisado com cautela! O que aqui rejeito são as alegações categóricas de que a razão de ouro está lá, ou que foi usada propositadamente. Notem, por exemplo, que a constante Pi (perímetro do círculo a dividir pelo seu diâmetro) aparece em várias manifestações físicas (sem relação aparente com círculos), e Pi/2 também é um valor próximo da razão de ouro… Quero com isto dizer que não tem que ser sempre a razão de ouro a responsável pela harmonia (existem mais números “especiais” em Matemática que têm uma relação directa com a Natureza). Sem que haja provas de uma convergência para o número de ouro, nem uma razão lógica para que o número de ouro se manifeste, não se devem tirar conclusões. Notem que caso a razão de ouro fosse a “fórmula mágica” para criar obras artísticas de qualidade superior, os artistas que a estudaram teriam certamente começado a usá-la com maior regularidade.
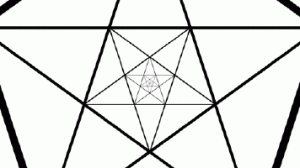
6 – Sexta alegação: existe uma relação entre o número de ouro e os pentágonos, bem como pentagramas e outras construções geométricas.
VERDADEIRO! Como já devem ter reparado, as alegações de carácter matemático tendem a ser todas verdadeiras, isto porque, naturalmente, quem as inventou sabia de Matemática…
Também neste caso é possível encontrar uma noção de infinito, como podem ver na imagem (dentro de cada pentagrama podem desenhar outro equivalente). A razão pela qual existe uma relação com o número de ouro é simples e está relacionada com o facto de o número de ouro ser (em parte) dada por uma raiz quadrada de 5. (Não me quero alongar demais, mas se o leitor tiver interesse, poderei dar mais detalhes em comentário.)
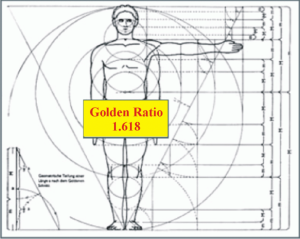
7 – Sétima alegação: a razão dourada dá-nos as proporções do corpo humano, podendo ser encontrada na face humana, em relações entre certos comprimentos que caracterizam o corpo humano, dentes, etc..
FALSO! É bem sabido que o corpo humano varia entre indivíduos, e embora algumas proporções se aproximem de facto do número de ouro, isso não chega para fazer afirmações definitivas. Até pode ser que algumas proporções efectivamente convirjam por razões biológicas para o número de ouro, contudo tal nunca foi demonstrado.
Assim, as imagens seguintes não passam de wishful thinking:
8 – Oitava alegação: existe uma relação entre o número de ouro e o mundo dos fractais.
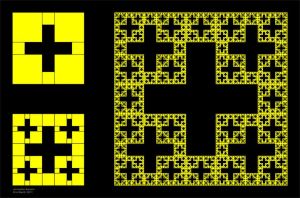
VERDADEIRO! Preparem-se para ficarem completamente maravilhados com esta relação! Antes de mais, convém relembrar que fractais são padrões que têm a particularidade de serem auto-similares em diferentes escalas. Ou seja, a ampliação de uma parte de um fractal, dá origem à imagem inicial:
Como podem constatar, as folhas de um feto são auto-similares, à medida que comparam diferentes escalas. (Ver mais sobre fractais no artigo sobre a Teoria do Caos.)
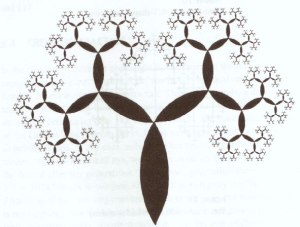
Para compreender a relação entre os fractais e o número de ouro, consideremos o seguinte fractal:
Este fractal que se assemelha a uma árvore, como podem ver, constrói-se com uma regra simples: começa-se com o “tronco” maior, o qual dá origem a dois menores, e depois cada um dos novos dá origem a outros dois… O problema fundamental ao tentarem construir este fractal está em saber escolher devidamente qual a diminuição de escala que devem fazer entre os novos troncos (ou folhas) e os anteriores. Se a razão entre o tronco velho e o tronco novo for muito grande, significa que o tronco novo é muito menor que o tronco velho, o que implica que usando este factor de escala, a árvore (fractal) “desaparece” muito depressa (ou seja, os “troncos filhos” tornam-se pequenos a uma taxa tal, que rapidamente se tornam muito pequenos). Caso a razão seja muito pequena, implica que os “filhos” são pouco menores que os “pais”, o que rapidamente conduzirá a uma sobreposição entre pais e filhos. A questão é: qual a razão óptima para fazer um bom preenchimento do espaço, sem que haja sobreposição? Como deve estar a adivinhar, a razão óptima entre o comprimento do tronco pai e do tronco filho coincide com o número de ouro! O mesmo acontece para qualquer fractal deste género, seja ele composto por triângulos, pentágonos, quadrados, etc.. A razão óptima de escalas coincide sempre com o número de ouro.
Isto não é apenas mais uma curiosidade matemática, pois as verdadeiras árvores lidam com este problema: ter folhas demasiado pequenas implica que a árvore não faça um bom aproveitamento da energia solar; por outro lado, ter demasiadas folhas conduz também a um minimizar da “performance” biológica, porque ter mais folhas tem um custo energético, o qual será injustificável caso as folhas estejam sempre à sombra.
Bom, tentei dar uma revisão geral sobre as principais alegações e mitos, porém deixei muitas outras de lado, porque o tema é muito vasto. É até eventualmente possível identificar o número de ouro, por exemplo, nos mercados financeiros. Se quiserem mais detalhes e exemplos podem ler o livro de Mario Livio, “The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number”. Também podem ver a palestra (em inglês) do professor Keith Devlin (clique para aceder ao vídeo).
*Nota: O modelo dos coelhos de Fibonacci também está envolto em mitos, aliás, o próprio Fibonacci o está. Primeiro, Fibonacci não se chamava Fibonacci, o nome foi-lhe atribuído mais tarde, por no seu grande livro, “”Liber Abbaci” (que revolucionou o sistema financeiro europeu e que é o seu grande legado), ter escrito, como era normal na época: “Filho de Bonacci”… Quanto ao modelo dos coelhos, ao contrário do que se afirma, Fibonacci não tinha qualquer interesse especial sobre este problema! Nem se pode dizer que seja um modelo “seu”, porque o problema e os números em causa já eram conhecidos antes de Fibonacci! Fibonacci apenas usou o problema no seu livro com propósitos educativos, para desafiar o leitor a pensar nos números… (Para terem uma ideia, no começo do livro, Fibonacci até explica o próprio significado dos algarismos, de modo a tornar o livro perceptível para quem nunca tinha aprendido aritmética na vida. Depois, apresenta inúmeros exemplos e problemas, para ajudar o leitor a começar a compreender os números e a saber usá-los. Muitos dos exemplos, naturalmente, são de carácter financeiro.)




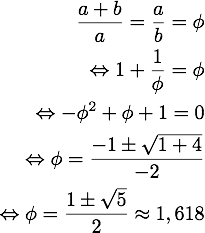
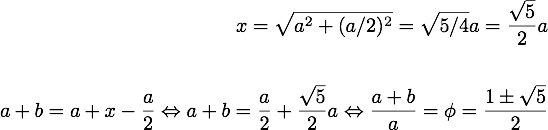
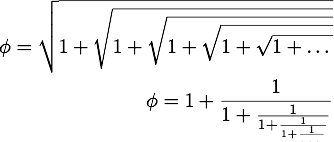
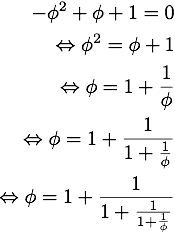












1 comentário
5 pings
Muito bem.
Um fractal reconhecido em muitas manifestações naturais…
[…] Número de ouro: 1.61803… (dízima infinita não-periódica) […]
[…] em alguns números em particular, nomeadamente o zero, o pi, e o número de ouro (ver também A Mitologia e a Verdade da Razão de Ouro). Nesta quinta e última parte vou-me debruçar sobre outros números especiais que serão […]
[…] este artigo, refiro ainda sumariamente o número de ouro, do qual já falei em detalhe no artigo A Mitologia e a Verdade da Razão de Ouro, e para o qual remeto o leitor. Aqui acrescento apenas um detalhe que não mencionei nesse artigo: […]
[…] fractal (D). (Recordo que já falei de fractais nos seguintes artigos: Teoria do Caos e A Mitologia e a Verdade da Razão de Ouro.) Até Mandelbrot a dimensão de um espaço era sempre um número inteiro: um ponto tem zero […]
[…] antes por Luca Pacioli (o matemático amigo de Leonardo da Vinci, que referi no artigo sobre o número de ouro, 1445-1517). Blaise Pascal (1623-1662) também o tentou resolver, falhou e por isso pediu a ajuda a […]