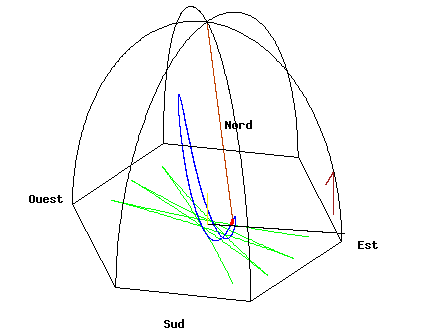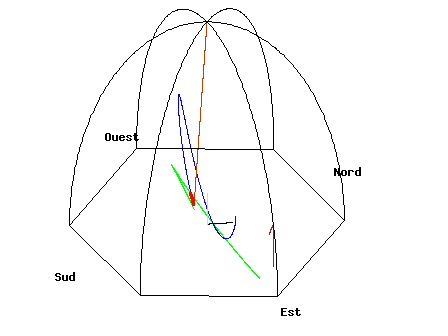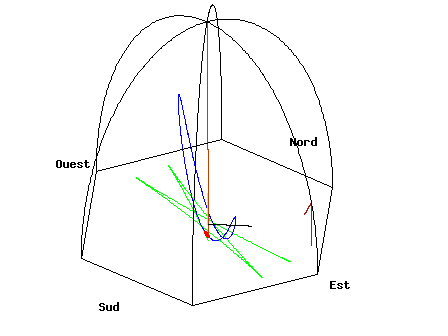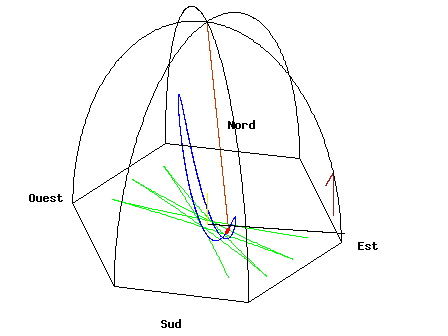
Na primeira parte falei-vos de pêndulos simples e referi que um Pêndulo de Foucault não é diferente desses pêndulos, exceptuando o facto de ser muito maior (normalmente usam-se “fios” de 12 a 30 metro). Neste caso o plano de oscilação vai rodando, como na imagem seguinte (o efeito está exagerado para se ver bem):
(A linha vermelha com o ponto vermelho representa o pêndulo, a linha azul é a trajectória do pêndulo no referencial que está a rodar juntamente com o próprio pêndulo, enquanto que a linha verde representa o percurso percorrido pelo pêndulo sobre o “chão” – o percurso da sua sombra, por exemplo. No final de ler o artigo ser-lhe-á mais fácil de compreender esta animação.)
Como também referi na primeira parte, esta rotação do plano é devida à rotação da Terra. Mas porquê?
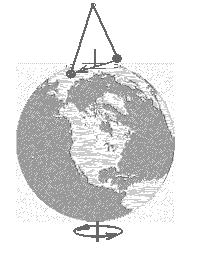
Para obterem alguma intuição, pensem num pêndulo a oscilar sobre o pólo norte* (ou pólo sul). Como o pêndulo oscila livremente, a Terra roda debaixo dele:
* O pólo norte é definido como o ponto onde o eixo de rotação intersecta a superfície do planeta. Notar que o pólo norte magnético não tem que necessariamente coincidir com este pólo e de facto não coincide.
Naturalmente, um observador que esteja na Terra irá acompanhar o movimento de rotação desta (sem notar que a Terra se está a mover), e se olhar para o movimento do pêndulo, verá o seu plano de oscilação a rodar. Se colocar um lápis na ponta do pêndulo, de tal modo que possa marcar a sua trajectória num “alvo” disposto debaixo do pêndulo, uma imagem semelhante à seguinte será desenhada (mais uma vez o efeito está exagerado):
Notem que isto é semelhante a desenharem numa folha de papel dois pontos, A e B, e a traçarem consecutivamente segmentos de recta a unir os dois pontos. Obviamente, os segmentos de recta coincidem sempre uns com os outros caso a folha esteja fixa (parada). Caso contrário, se colocarem a folha a rodar, uma de duas situações irá ocorrer: ou desenham uma linha curva para unirem na mesma o ponto A com o ponto B (que, ao contrário da folha, continuam fixos), ou se desenharem uma linha recta, o ponto A não irá encontrar o ponto B, por outras palavras, o plano de “oscilação” para traçar a linha parece ter mudado! Assim, isto é tudo uma questão de perspectiva, dependendo do referencial fixo que definem.
A animação seguinte ilustra bem o que acabei de explicar em cima:
A imagem pode ser interpretada da seguinte forma: uma esfera negra é deixada cair livremente (em linha recta, como se vê na imagem de cima), enquanto um disco (que contém o ponto vermelho) é rodado em segundo plano. Na imagem debaixo, o observador (ou uma câmara, por exemplo) está no ponto vermelho, ou seja, acompanha o disco a rodar, e por isso não observa qualquer movimento do disco. Consequentemente, a esfera preta parece-lhe ter uma trajectória curva. Notem que isto é em tudo semelhante ao pêndulo de Foucault, onde o observador está limitado ao referencial Terra que está a rodar e por isso vê o pêndulo a tomar uma trajectória inesperada.
Portanto, o importante a distinguir aqui é que existem dois referenciais: aquele que vê o movimento da Terra e do pêndulo (digamos: um observador no Sol), que é chamado referencial inercial; e aquele que acompanha o movimento da Terra e não a vê mover-se directamente, que é chamado sistema de referência em rotação.
Um aspecto interessante nisto é que o observador no referencial inercial (Sol), que vê o pêndulo a oscilar (num só plano) e a Terra a rodar, consegue descrever este sistema facilmente com as Leis de Newton do movimento (o movimento do pêndulo, em particular, será descrito de acordo com o que expliquei na primeira parte para um pêndulo simples, tendo em consideração a força gravítica e a força que o fio exerce sobre o peso que tem na ponta). No entanto, o problema parece já não ser tão simples para o observador que está na Terra, que vê o pêndulo a fazer uma trajectória estranha. A consideração das forças acima mencionadas não será suficiente, pois isso explica apenas um pêndulo a oscilar num só plano. Portanto, este observador terá que necessariamente assumir que existe pelo menos uma força adicional. Mas como pode ser que diferentes observadores vêem forças diferentes a actuar no mesmo objecto? A razão já a sabem: o observador que está a rodar em conjunto com a Terra não pode esquecer este facto! Tem por isso que considerar a existência de uma força fictícia. Chama-se fictícia porque “desaparece” se considerarmos um referencial inercial. No entanto, o seu efeito é real e mensurável num referencial não inercial.
A força fictícia que actua no pêndulo de Foucault é chamada de força de Coriolis. Para terem a noção do quão real é esta força fictícia, notem que, por exemplo, esta força tem um papel importante em meteorologia e oceanografia, estando envolvida na criação dos ciclones (caso o leitor tenha interesse, poderei dar mais detalhes nos comentários).
Sem querer entrar em grandes detalhes técnicos, lembro apenas que uma força é dada pela 2ª Lei de Newton, F=ma (ver Forças da Natureza), em que ‘F’ é a força, ‘m’ é a massa do objecto sobre a qual a força é aplicada (no caso do pêndulo, trata-se do peso colocado na ponta do fio), e ‘a’ é a aceleração desse objecto. A aceleração de Coriolis é dada pela seguinte expressão:
Nesta equação, ‘Ω’ é a velocidade angular do referencial em rotação (a Terra), e ‘v’ é a velocidade do objecto (pêndulo). Notar que ‘F’, ‘a’, ‘Ω’ e ‘v’ são vectores, ou seja, além de terem uma magnitude, têm também uma direcção associadas (ver a primeira nota a vermelho no artigo Leis da Conservação II). Na equação de cima, o sinal ‘x’ representa um produto vectorial, o que significa que o resultado da multiplicação dá origem a um vector com direcção perpendicular ao plano criado pelos dois vectores presentes na multiplicação, como explicado em Leis da Conservação II. Uma consequência disto verifica-se na direcção de rotação do plano de oscilação do pêndulo de Foucault, dependendo se estamos a observá-lo no hemisfério norte ou sul: no hemisfério norte o plano roda no sentido dos ponteiros do relógio, enquanto que no hemisfério sul o plano roda no sentido oposto (isto quando olhamos o pêndulo de cima). No hemisfério sul:
Alguns leitores talvez se estejam a recordar de uma noção relacionada com o que acabei de referir: a forma como a água flui ao escoar na sanita, por exemplo. Tem sido difundida a ideia de que a água escoa num sentido no hemisfério norte, e no sentido oposto no hemisfério sul devido ao efeito de Coriolis. Na verdade trata-se meramente de um mito, porque o efeito não é suficientemente forte para se verificar neste tipo de “experiência”. O sentido do vórtice é normalmente determinado por qualquer movimento inicial que a água já tinha, bem como a geometria do recipiente onde a água estava e por onde é escoada.
Já no que toca aos ciclones antes referidos, de facto estes têm uma direcção no hemisfério norte, e a contrária no hemisfério sul. (Num ciclone existe um movimento de ar de uma zona de maior pressão para uma de menor pressão – este movimento é deflectido devido à força de Coriolis, de tal modo que se forma uma espiral como na imagem abaixo.)
Ciclone polar sobre a Islândia.
Voltando à equação de cima, como disse, o efeito de Coriolis depende da direcção da velocidade do objecto (pêndulo), e da direcção de rotação do referencial (Terra). Como podem depreender, se o efeito tem direcções opostas em cada um dos hemisférios, no equador o efeito é nulo. Por outras palavras, no equador o pêndulo tem apenas um plano de oscilação que não muda de direcção (na verdade, a questão não é assim tão simples, porque a Terra não é uma esfera, pelo que é necessário considerar pequenas correcções). Sabendo a velocidade do pêndulo, a força de Coriolis (que se medem facilmente no pêndulo de Foulcault), e a velocidade de rotação da Terra, conseguimos determinar qual o ângulo que o vector velocidade do pêndulo faz com a velocidade angular da Terra. Por outras palavras, conseguimos saber a latitude do local onde o pêndulo está instalado! Resolvendo a matemática encontra-se a seguinte equação:
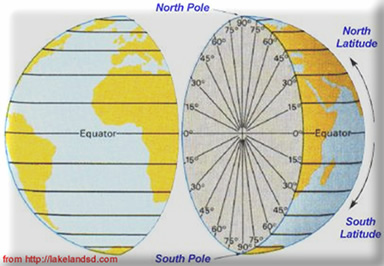
![]() ω é a velocidade angular de rotação do plano de oscilação do pêndulo (em graus por dia no sentido dos ponteiros do relógio), enquanto que φ é a latitude (ver imagem abaixo).
ω é a velocidade angular de rotação do plano de oscilação do pêndulo (em graus por dia no sentido dos ponteiros do relógio), enquanto que φ é a latitude (ver imagem abaixo).
No caso do pêndulo que está no Panteão de Paris, cuja latitude é definida pelo ângulo 48º, obtemos ω=360 sin (48º) = 267,5º. Ou seja, o plano de oscilação do pêndulo roda 267,5º num dia (aproximadamente)! Se forem visitar o Panteão e observarem o pêndulo duas vezes com um intervalo de uma hora, verificam que o plano de oscilação do pêndulo variou cerca de 11º (267,5/24=11,1). Notar que o ângulo é zero no equador, o que implica uma velocidade angular nula, como referido em cima. Por outro lado, no hemisfério sul os ângulos são negativos, pelo que a velocidade é negativa, o que denota o sentido contrário de rotação do plano. Finalmente, nos pólos o ângulo é de 90º (-90º no pólo sul), sendo o efeito máximo (sin (90º)=1), isto é, a velocidade angular é de 360º por dia, como é evidente, porque a Terra roda “debaixo” do pêndulo uma vez sobre si própria num dia – é a própria definição de dia (sideral).
Espero que o leitor reconheça agora o quão extraordinário o pêndulo de Foucault é na sua simplicidade: o baloiçar de um pêndulo consegue caracterizar a localização do pêndulo no planeta!









Últimos comentários