Paradoxos da Razão – Parte I

Um paradoxo é uma contradição, é como que uma falha lógica. Assim, como é que o pensamento racional poderá conduzir a paradoxos? A questão em si parece ser paradoxal, a menos que a razão nos pregue partidas.

Neste artigo vou discutir alguns dos mais famosos paradoxos que existem na Matemática. Note-se que a Matemática é meramente a forma que encontrámos de pensar com lógica em problemas abstractos. É uma linguagem especialmente desenvolvida para pensar e discernir padrões de forma compacta e coerente. “1+1=2” é o mesmo que pensar que “se juntarmos uma coisa com outra coisa, ficamos com duas coisas, independentemente do que sejam essas coisas”. Ao pensarmos em números, deixamos de pensar em “coisas particulares”, e estamos portanto a abstrair-nos delas. Assim, a Matemática permite-nos “elevar” o nosso pensamento para questões abstractas que seriam difíceis de distinguir sem esse nível de abstracção. Tente-se imaginar, por exemplo, o que seria tentar provar o Teorema de Pitágoras sem recorrer à linguagem matemática. Naturalmente, o ser abstracto não implica que seja “irreal” – o Teorema de Pitágoras, por exemplo, é bem real e comprovável fisicamente.

Os paradoxos que se seguem estarão organizados por ordem cronológica. Não irei discutir com grande detalhe as soluções, exactamente para que o leitor tenha a “liberdade” de pensar por si próprio.

Paradoxos de Zeno 

Zeno (ou Zenão) de Eleia (Itália) foi um filósofo pré-socrático que viveu entre 490 a.C. e 430 a.C. (mais ou menos). O seu paradoxo mais famoso é sobre a natureza do movimento, o qual segundo Zeno seria uma ilusão. Este paradoxo é contado da seguinte forma:

Imagine-se que o herói grego Aquiles queria disputar uma corrida com uma tartaruga. Como Aquiles era mais rápido que a tartaruga, esta começaria a corrida um pouco mais à frente que o Aquiles. Quem venceria a corrida? O leitor poderá pensar de imediato que se simplificarmos o problema, e considerarmos as velocidades de Aquiles e da tartaruga constantes, então, dando-se a partida em simultâneo, chegará primeiro aquele que demorar menos tempo a chegar à meta, o que dependerá das distâncias a percorrer, e das velocidades. Zeno, porém, pede ao leitor que pense de outra forma: Aquiles começa atrás da tartaruga, digamos, numa posição A, e a tartaruga começa numa posição B. Quando Aquiles chega à posição B, a tartaruga já terá chegado a uma posição C, mais adiante que B. Quando Aquiles chega à posição C, a tartaruga já vai numa posição D… E assim sucessivamente, ad infinitum. Deste ponto de vista, Aquiles nunca ultrapassa a tartaruga, consegue simplesmente aproximar-se cada vez mais dela.

Este aparente paradoxo é equivalente ao seguinte problema: imagine que está, digamos, a um metro do seu frigorífico e lhe é dada a possibilidade de se deslocar em saltos iguais a metade da distância entre si e o frigorífico (depois de cada salto). No primeiro salto desloca-se ½ da distância inicial, a seguir ¼ (metade de um meio), depois 1/8, e assim sucessivamente. Um número finito de saltos não será suficiente para alcançar o frigorífico!

Note-se, porém, que o frigorífico é “alcançado no infinito”. Recorde o artigo em que provei que 0.9(9)=1. A soma da série infinita ½ +¼+1/8+… é equivalente à última fórmula presente nesse artigo, em que r=½, e com o índice ‘n’ a começar em 1:

E, portanto, quando r=½:

Este paradoxo está intrinsecamente relacionado com a relação entre as noções de contínuo e discreto: o contínuo é “preenchido” por um número infinito de elementos discretos. Serão o espaço e o tempo contínuos ou discretos? Será a continuidade meramente uma ilusão criada pelo nosso cérebro? Estas são questões antigas em Filosofia. Para já a Física ainda não consegue afirmar com certezas se as dimensões do nosso universo são contínuas ou discretas.

 O Paradoxo da Roda de Aristóteles

Este paradoxo está relacionado com o acima exposto. O problema em causa aparece no mais antigo livro de engenharia conhecido, “Mechanica”, que é atribuído a Aristóteles, mas que pode ter sido escrito por outra pessoa, à partida da sua escola (Estratão de Lâmpsaco (Turquia), aluno de Aristóteles, é outro candidato).

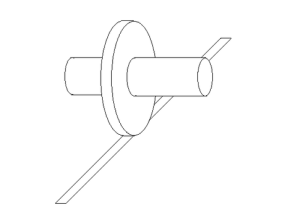
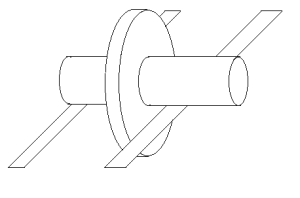
A animação de cima ilustra o paradoxo: duas circunferências concêntricas, de raios diferentes, têm uma relação de um para um entre todos os seus pontos. Logo, se estiverem “coladas”, ao rodar-se uma circunferência 360º, a outra também roda 360º. Como na animação, poderemos fazer as circunferências rodar de modo a percorrer uma dada distância – como existe uma relação de um para um entre os pontos das duas circunferências, parece ser indiferente fazer as circunferências rodar sobre a linha horizontal de baixo (em que a circunferência maior está “apoiada”), ou sobre a linha horizontal de cima (onde está “apoiada” a circunferência menor). Se for mais fácil, podem imaginar antes o sistema assim:

A relação de um-para-um entre os pontos das duas circunferências leva-nos a pensar que se rodarmos o sistema, por exemplo, 360º (uma volta completa), ele terá viajado a mesma distância quer esteja “apoiado” sobre a circunferência maior, quer esteja sobre a circunferência menor, tal como na animação de cima.

É claro que isto está errado! O percurso percorrido por uma circunferência que roda 360º (sem deslizar) é exactamente igual ao seu perímetro, o qual, como sabem, é igual ao diâmetro a multiplicar pela constante pi (aproximadamente 3.14). Se as duas circunferências têm diâmetros diferentes isso implica que os percursos percorridos sejam diferentes!

O que está aqui implícito é que duas curvas não têm necessariamente o mesmo comprimento simplesmente por terem uma correspondência de um-para-um entre os seus pontos! Note-se que um segmento de recta tem sempre um número infinito de pontos, independentemente do seu tamanho. Por outro lado, é sempre possível fazer uma relação de pontos de um-para-um entre dois segmentos de recta de comprimentos diferentes, ou até mesmo entre um segmento de recta e uma recta (cujo comprimento é infinito).

Todas estas noções são difíceis de compreender porque envolvem infinitos e só ficaram bem estabelecidas com o contributo de Georg Cantor (matemático russo que viveu entre 1845 e 1918) sobre números transfinitos (sobre os quais talvez venha a falar um pouco mais num artigo futuro).

O Problema da Corda à Volta da Terra 

Este problema não é propriamente um paradoxo, nem tem um grau de complexidade comparável aos anteriores, contudo é igualmente fascinante por ser bastante contra-intuitivo.

Comece por imaginar que coloca uma corda à volta do “equador” de uma bola de futebol. Quão maior teria que ser a corda caso quisesse que a corda ficasse a um centímetro da superfície da bola (também em relação ao equador)? (Considere, por exemplo, que a bola tem uns 25 cm de diâmetro.)

Imagine de novo o mesmo problema, mas use o planeta Terra em vez da bola de futebol. E agora, quão maior teria que ser a corda para ficar a um centímetro da superfície da Terra? (A Terra tem um diâmetro de cerca de 12 700 km.)

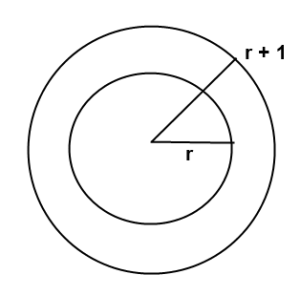
Parece evidente que o pedaço de corda que temos que acrescentar no segundo caso, para que a corda fique a um centímetro do equador da Terra, deverá ser muito maior que o pedaço de corda que é necessário acrescentar à corda que envolvia a bola de futebol, certo? Errado! Se fizer as contas vai ver que o comprimento de corda que precisa adicionar em cada um dos casos é igual! Em geral temos uma circunferência de raio R, cujo perímetro é 2 pi R. Caso queiramos fazer uma circunferência com raio ‘R+1’, o perímetro desta circunferência é 2 pi (R+1):

O perímetro da circunferência de fora é ‘2 pi’ maior que o outro (2 pi (R+1)-2 pi R=2 pi), independentemente do raio R em causa! Neste exemplo adicionámos uma unidade, ou seja, pode ser um centímetro, como em cima, e nesse caso a corda mede mais 2 pi (aproximadamente 6.28) centímetro para estar a um centímetro do equador da bola, ou da Terra!

Sintam-se à vontade para discutir os paradoxos nos comentários. Na próxima parte irei discutir outros paradoxos famosos.