Um paradoxo é uma contradição, é como que uma falha lógica. Assim, como é que o pensamento racional poderá conduzir a paradoxos? A questão em si parece ser paradoxal, a menos que a razão nos pregue partidas.
Na parte I falei-vos dos paradoxos de Zeno, do paradoxo da roda de Aristóteles, e do problema da corda à volta da Terra. Nesta segunda parte vou abordar o Paradoxo de São Petersburgo, o Princípio da Casa de Pombos, e a Fita de Möbius. Na verdade nenhum deles é verdadeiramente um paradoxo, mas são suficientemente “estranhos” para o parecerem!
Paradoxo de São Petersburgo
Proponho-lhe jogarmos o seguinte jogo: lançamos a moeda ao ar, se sair coroa, dou-lhe 2€. Se sair cara e coroa dou-lhe 4€. Se sair cara, cara, e coroa, dou-lhe 8€. Ou seja, o jogo acaba quando sai coroa, e eu dou-lhe 2^n €, em que ‘n’ é o número de vezes que a moeda foi lançada ao ar (por exemplo, para cinco lançamentos, n=5, 2^5=2x2x2x2x2=32). Quanto me deverá você pagar antes de aceitar o meu desafio para que seja justo jogarmos o jogo? Por outras palavras, quanto dinheiro devo eu exigir que você me pague antes de jogarmos, para que a probabilidade de eu ficar a ganhar dinheiro com o jogo seja semelhante à probabilidade de você enriquecer com o jogo?
De forma empírica seríamos levados a indicar um valor não superior a 20€, mais ou menos, visto que a probabilidade de ganhar mais que 20€ (sair pelo menos 4 vezes seguidas cara) parece já bastante baixa: 1/32, cerca de 3%. Contudo, devemos reparar que quanto menor é a probabilidade, maior é o ganho.
A questão resume-se então a tentar estimar quanto é que você poderá ganhar com o jogo. Com 50% de probabilidade irá receber 2€; com 25% de probabilidade irá receber 4€; com 12.5% de probabilidade irá receber 8€; e assim sucessivamente. Para quem sabe um pouco de matemática, em particular de estatística, saberá que o valor esperado do montante a receber pelo jogador é dado pela soma dos ganhos a multiplicar pelas respectivas probabilidades:
Valor esperado = 2x(1/2)+4x(1/4)+8x(1/8)+… = 1+1+1+1+1+…= infinito
O montante que você poderia receber diverge – não tem um limite! (Em termos práticos existe sempre um limite, claro.) Isto significa que você deveria aceitar jogar independentemente do valor (finito) que eu lhe exigisse! Mais uma vez (ver parte I) temos uma noção contraditória relacionada com o infinito! Naturalmente, se levarmos em conta as limitações monetárias dos intervenientes, já será possível calcular o valor justo para entrar no jogo.
Este problema foi discutido em 1738 pelo matemático, físico e médico, Daniel Bernoulli, num artigo publicado numa revista científica de São Petersburgo (Commentaries of the Imperial Academy of Science of Saint Petersburg), daí o nome de Paradoxo de São Petersburgo. Note-se que de acordo com a Teoria de Jogos, um “jogador racional” deve aceitar pagar um dado montante para entrar num jogo se o lucro expectável for superior ao montante exigido. Neste caso, em condições idealizadas, o jogador racional (matemático) aceitaria sempre jogar. Em contraste, o nosso bom senso dir-nos-ia para não jogar se a quantia exigida implicasse uma probabilidade relativamente baixa de beneficiarmos com o jogo.
Existem diversas resoluções para este paradoxo, mas não as menciono aqui para que o leitor tenha uma maior liberdade criativa para pensar neste problema.
Princípio da Casa de Pombos
Este princípio é também conhecido por teorema de Dirichlet ou princípio das gavetas de Dirichlet, tendo sido introduzido em linguagem matemática pelo matemático alemão Johann Dirichlet em 1834. Este princípio é extremamente intuitivo e do mais simples que pode haver: se tivermos um número X de casas de pombos, e um número Y de pombos, então haverá casas de pombos com mais de um pombo, caso o número de pombos seja superior ao número de casas (Y>X).
Com base neste princípio posso dizer-lhe que é possível encontrar duas pessoas em Portugal com o mesmo número de cabelos! O número de cabelos de uma pessoa é sempre (bastante) inferior a um milhão (X=1000 000), e em Portugal existem cerca de dez milhões de habitantes (Y). Então, como Y>X, tem que haver indivíduos com o mesmo número de cabelos.
Curioso como um princípio tão simples consegue conduzir-nos a conclusões que parecem transcender o princípio. Caso tenha ficado confundido com o exemplo de cima, exponho um exemplo mais simples: quantas pessoas precisa reunir para que tenha a certeza absoluta de que pelo menos duas fazem anos no mesmo dia? Neste caso o número de pombos corresponde aos dias de aniversário, portanto X=366 (contando com o 29 de Fevereiro). Para que possa usar o princípio, precisa que Y seja maior que X, em que Y neste caso é o número de pessoas. Para que Y seja maior que X, basta que Y seja 367. Assim, se reunir 367 pessoas garante que pelo menos duas delas tenham o aniversário no mesmo dia.
Realço que este princípio dá-nos certezas e não apenas probabilidades. Não é estritamente paradoxal, mas é de certo modo contra-intuitivo.
Fita de Möbius
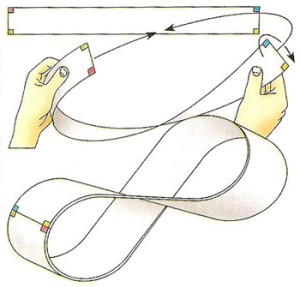
A imagem acima representa a chamada Fita de Möbius. Analise-a bem, e experimente a imaginar-se a percorrer a superfície da fita, ou a percorrer a sua linha delimitadora. Chegará à conclusão que a fita é uma superfície só com um lado, e só tem uma linha que a delimita!
Não se trata apenas de uma construção gráfica! Desafio o leitor a fazer uma fita de Möbius! Como? O material que precisa é o seguinte: uma folha A4, e fita-cola (ou um agrafador). Para ajudar na construção, traga também uma caneta e uma tesoura (embora sejam desnecessários).
Primeiro faça uma pequena fita com a folha A4, digamos um rectângulo com cerca de 30 cm por 3 cm. Dum lado da fita, numa extremidade escreva um A, e na outra extremidade escreva um B. Vire a fita ao contrário e escreva um C na extremidade do lado do B, e um D na extremidade do lado do A. Com a fita faça um anel. Ao juntar as extremidades fica com o A e o B de um lado, e o C e o D do outro. Para transformar o anel numa fita de Möbius tem que virar uma das pontas de modo a ficar com B e o D do mesmo “lado” (o que faz com que o A e o C fiquem também juntos, claro). Cole a fita com as extremidades nessa posição e terá uma fita de Möbius.
Não há registos sobre esta curiosa forma geométrica até ao século XIX! Tanto quanto se sabe, só em 1858 é que o matemático alemão August Möbius descobriu a “sua fita”. Note-se que uma consequência de a fita de Möbius só ter um lado é que se tentar pintar um “lado” da fita acaba por a pintar toda.
A fita de Möbius não é apenas uma curiosidade com aplicações em arte. Trata-se de um “elemento” fundamental em Matemática, e (de certo modo consequentemente) tem aplicações em Física (nomeadamente na estrutura de moléculas).
Esta forma matemática não tem nada de paradoxal, contudo temos que concordar que é suficientemente estranha para parecer à primeira vista uma forma impossível.
Sintam-se à vontade para discutir os “paradoxos” nos comentários. Na próxima parte irei discutir outros paradoxos famosos.











4 comentários
3 pings
Passar directamente para o formulário dos comentários,
A referência a “29 de Setembro” no texto é uma gralha não é? ( ou será um paradoxo )
)
Author
Corrigido. Obrigado.
Cutting a Möbius Strip in Half
Animation made by me using Mathematica 7 and CamStudio 2.0.
https://www.youtube.com/watch?v=MWrfQwrUWnM
In a simple demonstration, Radcliffe Institute fellow and mathematician Tadashi Tokieda uses paper, tape, and scissors to get some surprising results…
https://www.youtube.com/watch?v=5xLFf_SwaK4
Sugestão:
The Mobius Time Loop
http://www.cix.co.uk/~antcom/mtl.html
August Ferdinand Mobius a 19th century German mathematician and astronomer found that by joining the two ends of a piece of paper together to form a loop BUT twisting the ends before they were joined a continuous loop of only one side was formed.
With the Grandmother paradox we essentially have a time with a Grandmother and a time without.
Also if you follow the description in quotes at the top of this page it appears that one follows the other and loops back to the beginning.
We can use the Mobius Strip and adapt it to “show a possible interpretation” of how Time is twisted in the Grandmother paradox.
This is difficult to show on a two-dimensional computer screen or paper so you will need to construct one by printing out the diagram below.
You will need scissors, sticky tape and glue. Follow the instructions and then read the description that follows below.
Esta sugestão dum “Nobius Time Loop” de papel vai no sentido de responder a esta parte de um dos debates sobre o Interstellar, neste link:
http://www.astropt.org/2014/11/24/a-ciencia-e-o-filme-interestelar-os-acertos-e-os-erros/#comments
Lembram-se como é usada uma folha de papel numa cena do filme para ilustrar o wormhole, quando se dobra uma folha de papel e depois é furada por uma lapiseira? Quem “dobra” (a gravidade faz isso) uma folha de papel, também (se quiser) a pode torcer (uma tira de papel neste caso) com uma rotação de 180 graus…
Citação de alguns comentários sobre os “Acertos e Erros” do Interstellar:
Marcelo
08/04/2015 em 03:58 (UTC 1) Link para este comentário
Responder
Eu acho que não existem muito nexo na forma em que ele encontra a NASA no filme.
Vamos lá, ele tem uma grande aventura, que se inicia graças ao fato dele ter encontrado a NASA. Nesta aventura ele viaja em buraco de minhoca, encontra outros mundos e cai em um buraco negro….então ele fica preso em uma dimensão X. Nessa dimensão ele se depara atrás do quarto da filha. Então ele começa a se comunicar com ela. E ai, entra o ponto faz tudo perder o nexo para mim. Em um dado momento, ele se comunica com a filha, mandando as coordenadas em binário de onde fica a base da NASA.
Essa informação é interpretada por ele mesmo na terra, que consegue decifrar a mensagem e encontrar a NASA, e ai tudo começa novamente.
Massss, para mim a grande questão é: Como ele pode descobrir onde fica a base da NASA, momento que dá início a toda viagem, se ele mesmo é o responsável por passar a informação para ele!!
Qual foi o momento INICIAL em que ele foi ao espaço?Vocês entendem, não faz sentido, não tem coesão. É como o John Connor, em O Exterminador do Futuro, enviar um amigo do Futuro para proteger a sua mãe e esse amigo ‘e o seu PAI!!!!
Eu realmente gostei de Interstellar, mas esse ponto ai, para mim, foi um “erro” primário.
Fabio
15/04/2015 em 15:24 (UTC 1) Responder
Isso faz todo o sentido! ou melhor, não faz sentido algum! Isso me parece um ponto muito falho do filme. Para mim perde completamente a coesão de existência temporal. Como o amigo acima disse, QUANDO É O INÍCIO REAL!!?!
Juliana
13/04/2015 em 05:30 (UTC 1) Responder
Marcelo!!! Até q enfim encontrei alguém com a mesma dúvida q eu!!! Por favor, alguém sabe a resposta? É tão óbvio q não enxergo????
Embora goste bastante destes diagramas, ainda continuo á procura de algum que tenha sido feito em 3D com um anel de Mobius:
http://www.astropt.org/2015/04/08/linha-temporal-no-filme-interestelar/#comments
Para quem quiser tentar aprofundar o tema:
http://pt.wikipedia.org/wiki/Cone_de_luz / http://en.wikipedia.org/wiki/Light_cone
http://en.wikipedia.org/wiki/Causal_structure#Causal_structure
http://en.wikipedia.org/wiki/Closed_timelike_curve
If CTCs exist, their existence would seem to imply at least the theoretical possibility of time travel backwards in time, raising the spectre of the grandfather paradox, although the Novikov self-consistency principle seems to show that such paradoxes could be avoided.
http://en.wikipedia.org/wiki/Grandfather_paradox / http://pt.wikipedia.org/wiki/Paradoxo_do_av%C3%B4
Aliás, para além dos filmes da série Terminator, referidos, há um outro filme em que é retratado um “Mobius Time Loop” que é este: http://en.wikipedia.org/wiki/12_Monkeys / http://pt.wikipedia.org/wiki/Twelve_Monkeys
“…she makes eye contact with a small boy: the young James witnessing the scene of his own death, which will replay in his dreams for years to come…”
Também gosto deste filme pelo seu “realismo” pois acontece algo (uma certa falta de pontaria) que seria (bastante?) plausível de ocorrer se essa tecnologia existisse:
“James Cole é primeiramente mandado por acidente ao ano errado…” Dr. Kathryn Railly: You had a bullet from World War I in your leg, James! How did it get there?
Uma curiosidade sobre a origem duma parte dos aparelhos (futuristas) de 2030, “estilizados” no filme:
In the beginning of the film, Cole is brought into the interrogation room and told to sit in a chair attached to a vertical rail on the wall. A sphere supported by a metal armature is suspended directly in front of him, probing for weaknesses as the inquisitors interrogate him.
Architect Lebbeus Woods filed a lawsuit against Universal in February 1996, claiming that his work “Neomechanical Tower (Upper) Chamber” was used without permission.
Woods won his lawsuit, requiring Universal to remove the scenes, but he ultimately allowed their inclusion in exchange for a “high six-figure cash settlement” from Universal.
Real art described in fiction.
http://artinfiction.tumblr.com/post/98668301916/neomechanical-tower-upper-chamber-by-lebbeus
Lebbeus Woods and 12 Monkeys
http://lifewithoutbuildings.net/2006/09/lebbeus-woods-12-monkeys.html
Por último:
Este link a seguir leva a uma página sobre a série “Lost” (nunca tive paciência de ver todos os episódios) onde está um gráfico muito simples com um tempo de 1977 a 2007 e com dois universos paralelos A e B que correspondem a cada lado da banda de papel antes de se torção de 180 graus:
http://theoreticalisland.blogspot.pt/2009/05/moebius-history.html
http://en.wikipedia.org/wiki/Lost_(TV_series) / http://pt.wikipedia.org/wiki/Lost_(s%C3%A9rie_de_televis%C3%A3o)
Curiosamente, até na interpretação desta (simples?) série de TV, se pode observar fenómenos de pseudo-ciência:
O derradeiro episódio de Lost, intitulado “The End”, dividiu a opinião dos fãs da série, ao deixar sem respostas muitos mistérios propostos ao longo de seis anos para focar apenas em seus personagens, “comprovando definitivamente” que Lost é uma série que “fala sobre pessoas e suas diversas relações”, utilizando elementos mistícos e enigmáticos apenas como meio de conduzir estas pessoas à lugares e situações diversas para que “descubram mais sobre seu próprio eu” e a sua própria redenção.
Teorias desmistificadas
O coração da série é uma história complexa e crítica que desova inúmeras questões não resolvidas.
Incentivada pelo elenco e escritores de Lost, que muitas vezes interagem on-line com os fãs, leitores e críticos de Televisão tem tentado criar teorias generalizadas, numa tentativa de desvendar os mistérios.
As teorias dizem sobretudo a respeito da natureza da ilha, a origem do “monstro” e dos “Outros”, o significado dos números e as razões da queda do avião e a sobrevivência de alguns passageiros..
Várias das mais comuns teorias criadas por fãs foram discutidas e rejeitadas pelos criadores da série, as mais comuns sendo que os sobreviventes do Vôo 815 estão mortos ou no purgatório.
Esta foi expressamente negada por J.J. Abrams.
Além disso, Lindelof rejeitou especulações de que naves espaciais ou aliens estavam influenciando os acontecimentos na ilha, ou que tudo não passava de um delírio colectivo.
Carlton Cuse negou a teoria de que a ilha era um reality show da TV e que os sobrevientes seriam náufragos e Lindelof, muitas vezes, já refutou a teoria de que o “monstro” é uma nuvem nanobótica semelhante a que estava presente no livro Prey de Michael Crichton.
Legal os seus paradoxos, ou quase paradoxos, beleza.
[…] de Zeno, do paradoxo da roda de Aristóteles, e do problema da corda à volta da Terra. Na parte II abordei o Paradoxo de São Petersburgo, o Princípio da Casa de Pombos, e a Fita de Möbius. […]
[…] de Zeno, do paradoxo da roda de Aristóteles, e do problema da corda à volta da Terra. Na parte II abordei o Paradoxo de São Petersburgo, o Princípio da Casa de Pombos, e a Fita de Möbius. […]
[…] de Zeno, do paradoxo da roda de Aristóteles, e do problema da corda à volta da Terra. Na parte II abordei o Paradoxo de São Petersburgo, o Princípio da Casa de Pombos, e a Fita de […]