Regressão de Leis no Universo

Uma das assunções fundamentais em Ciência é que as leis que governam o funcionamento do universo são imutáveis. Poderá, por isso, deduzir que a “regressão” do título não tem o significado de retrocesso, mas antes um outro significado mais técnico. Em Matemática, “regressão” é um método que permite inferir a relação entre variáveis. Trata-se de uma técnica estatística crucial em Ciência para avaliar relações entre medidas experimentais. Este artigo terá alguns detalhes um pouco técnicos, por isso exorto o leitor a não se coibir de usar os comentários para pedir mais esclarecimentos caso a presente explicação não lhe pareça suficiente.

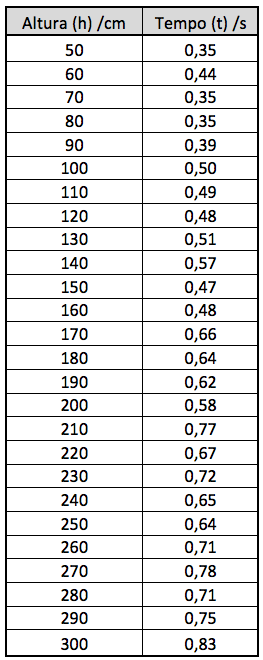
Como deverá ser do seu conhecimento, a aceleração gravítica pode ser considerada constante junto à superfície do planeta. Vamos imaginar que queremos verificar este facto através de experiências. O que fazemos? O mais simples será deixar cair objectos e medir o tempo que demoram a chegar ao chão. Uma vez que sabemos que existe resistência do ar e que a mesma é tanto maior quanto maior for a área “varrida” pelo objecto, poderíamos usar pequenas esferas (a forma também é relevante). A aceleração gravítica é independente da massa, portanto não temos que nos preocupar com isso (se fizessem a experiência na rua, o vento seria um factor a considerar e nesse caso a massa já seria importante). Precisaríamos ainda de um cronómetro e de uma fita métrica para medir as alturas das quais deixaríamos cair as esferas. Como estamos só a imaginar a experiência vamos desprezar o problema de conseguir medir com precisão os tempos de queda. Galileu resolveu esta questão fazendo a experiência em calhas inclinadas, o que aumenta o tempo de “queda”. Porém, por uma questão de simplicidade, vou assumir que conseguiríamos de facto medir os tempos (com detectores electrónicos, por exemplo). Assim, os dados experimentais que registaríamos seriam alturas e respectivos tempos de queda. Imaginando que mediríamos alturas entre 50 centímetros até três metros, obteríamos uma tabela de valores semelhante à seguinte:

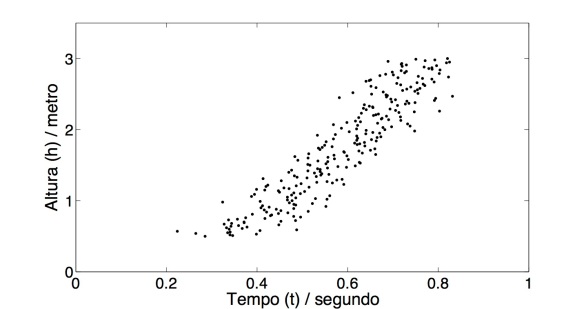
Como é evidente, em média, à medida que a altura aumenta, o tempo de queda também aumenta. Há, contudo, excepções nesta tabela que têm o objectivo de ilustrar os erros de medida que seriam cometidos. Note-se que mesmo de uma altura de três metros, o tempo de queda é inferior a um segundo! Um outro aspecto a notar é o facto de o tempo não aumentar de forma linear com a altura. Isto é, se a relação fosse linear, o tempo medido de uma altura de dois metros seria aproximadamente o dobro do tempo medido de uma altura de um metro. É comum disporem-se os dados experimentais em gráficos, uma vez que a sua análise qualitativa é mais rápida:

Cada ponto representa uma altura e correspondente tempo de queda (na tabela coloquei apenas alturas de 10 em 10 cm, mas nesta figura coloquei de 1 em 1 cm, o que significa que temos 251 pontos). É aparente uma certa dispersão dos pontos. Isto é algo expectável de observar em qualquer experiência onde erros experimentais não sejam desprezáveis, o que é de resto sempre o caso, porque qualquer instrumento de medida tem um limite de resolução, o que significa que fazemos sempre arredondamentos mesmo que os quiséssemos evitar. Por exemplo, se a nossa fita-métrica estiver dividida até a uma escala de centímetros, não podemos esperar conseguir determinar distâncias de milésimos de milímetros (micrómetros). Porém, não é difícil de imaginar que quando deixámos cair a nossa esfera de uma altura de 100 centímetros, a altura poderia ser na verdade de 100.0107 centímetros, por exemplo. Estes 0.0107 centímetros podem não fazer grande diferença, não obstante trata-se de um erro que não devemos esquecer (noutras experiências mais sensíveis pode fazer toda a diferença). Para obter estes dados, porém, assumi que o erro experimental estava principalmente na medição do tempo, sendo que podem atribuir o erro à resistência do ar, e à falta de precisão dos detectores usados. (Os dados aqui presentes são artificiais: em vez de terem sido obtidos através da referida experiência, foram antes calculados através de um programa de MatLab criado por mim – least_squares.)

À primeira vista os pontos até podem parecer distribuir-se mais ou menos de forma linear, o que desde logo nos chama a atenção para não tirarmos conclusões precipitadas de uma análise a “olhómetro”! Antes de prosseguirmos no estudo destes dados convém ter uma noção daquilo que esperamos obter. Ora, se a aceleração gravítica (g) é constante, então a velocidade (v) aumenta linearmente com o tempo (t):

Para quem sabe cálculo integral é fácil de reconhecer que se integrarmos no tempo esta equação obtemos a relação que procuramos

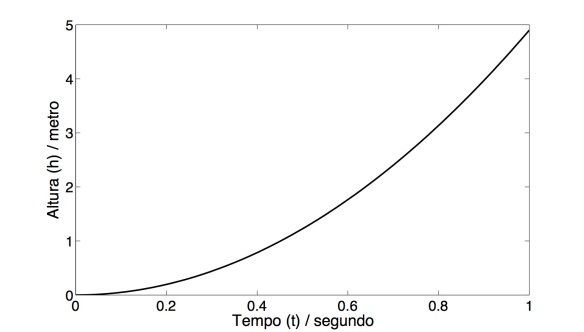
em que h corresponde à altura de onde deixamos cair a esfera. De acordo com o que tinha sido antecipado, a relação não é linear porque o tempo (t) está ao quadrado:

Este tipo de curva chama-se parábola.

Agora que sabemos a teoria, como é que podemos determinar a aceleração gravítica g através dos nossos dados experimentais? Se o leitor teve aulas de laboratório é provável que saiba a resposta: podemos fazer uma regressão linear dos nossos dados experimentais. Para o fazer, primeiro temos que efectivamente ter uma relação linear entre as variáveis. Como a relação não é linear é necessário criar novas variáveis. Rearranjando a equação de cima:

e comparando a uma equação linear:

ficamos com:

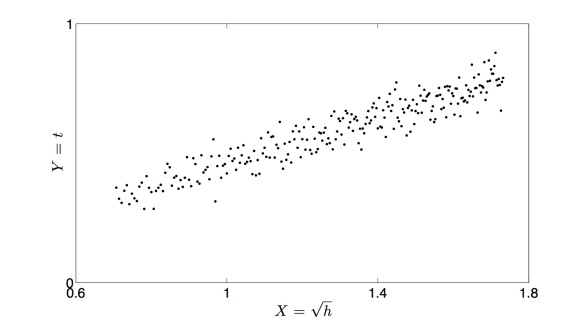
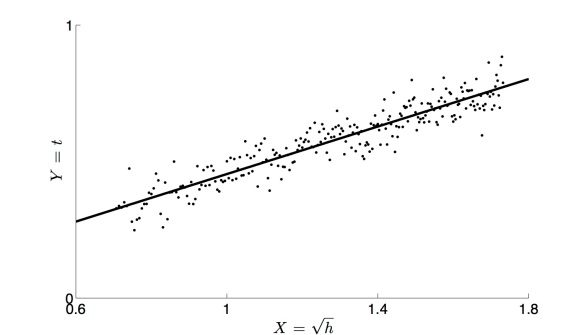
O que acabo de fazer é chamado de linearização. Trata-se dum método através do qual se cria uma relação linear entre variáveis (X e Y) que estão relacionadas com as nossas variáveis iniciais (h e t). O leitor pode reconhecer que era também possível linearizar assumindo Y igual a h, e X igual ao quadrado de t, com m=2g e b=0. A razão pela qual não escolhi essa linearização deve-se ao método que quero usar em seguida para achar a melhor recta que passe pelos pontos (X,Y). Como a relação dos dados experimentais entre a altura e o tempo não correspondia de forma exacta à parábola esperada pela teoria, é claro que os pontos (X,Y) também não perfazem uma recta perfeita:

Para encontrar a melhor recta que descreva estes pontos podemos usar o famoso Método dos Mínimos Desvios Quadrados, o primeiro método matemático a ser criado para obter uma regressão. Para aplicar este método é necessário assumir que a incerteza está concentrada na variável Y (daí que tenha escolhido Y como função de t, e não de h). A ideia chave do método consiste em achar a melhor recta de ajuste cuja distância total dos pontos à recta seja mínima (em geral pode ser uma curva qualquer, não necessariamente uma recta). Esta “distância total” corresponde à soma dos resíduos ao quadrado, em que um resíduo é a distância no eixo Y entre um dado ponto e o respectivo ponto na recta para o mesmo X. Aplicando o método aos nossos dados pseudo-experimentais obtemos a seguinte recta:

Este método calcula o declive (m) da recta, bem como a sua ordenada na origem, isto é, o ponto no qual a recta intersecta o eixo dos YY (b). Na nossa análise estamos interessados em conhecer qual a aceleração gravítica, a qual, como vimos, se relaciona com o declive desta recta:

logo

Como , então . O valor real é aproximadamente . Para comparar o valor encontrado e o valor real faltava ainda estimar qual a imprecisão que temos na nossa estimativa tendo em conta que os pontos experimentais são afectados por erros de medição. Não vou, porém, preocupar-me com isso aqui, ainda que seja um aspecto de extrema importância: se a imprecisão for elevada, o facto de haver uma aparente concordância entre o valor obtido e o valor esperado tem que ser considerado uma mera coincidência e a conclusão a tirar é que é necessário melhorar o método experimental. Uma outra consideração a ter é o quão bem os dados experimentais podem ser de facto ajustados a uma recta. O método dos mínimos desvios quadrados permite-nos estimar o chamado coeficiente de determinação o qual nos dá a correlação dos pontos à recta. Para o nosso exemplo obtive:

Se a correlação dos pontos à recta fosse perfeita obteríamos um coeficiente igual a 1. Este 0.88 por si só não nos dá grande informação, porém permite-nos comparar esta regressão linear com outras regressões possíveis (em geral, se o coeficiente for inferior a 0.8, a regressão é má, enquanto que se for superior a 0.9 é boa, ainda que sem outras informações estes limites sejam puramente arbitrários). Poderíamos, por exemplo, tentar comparar esta regressão simples com uma outra em que se usasse um modelo mais realista que considerasse a resistência do ar na esfera (a equação que relacionaria a altura e o tempo de queda seria diferente e como tal a regressão também seria diferente).

O método dos mínimos desvios quadrados foi desenvolvido pelo matemático alemão Carl Friedrich Gauss (1777-1855) quando este tinha apenas 18 anos. Em 1801, Gauss usou o método para prever a localização futura do planeta anão Ceres (o maior corpo celeste da cintura de asteróides entre Marte e Júpiter). Ceres tinha sido descoberto um ano antes pelo astrónomo italiano Giuseppe Piazzi (1746-1826), mas passado pouco tempo já não era possível observá-lo por ter “desaparecido” atrás do Sol. Assim, a previsão de Gauss permitiu determinar quando e aonde (no céu) seria possível observá-lo de novo. Na verdade, Gauss manteve o seu método secreto durante alguns anos de forma a ter vantagem sobre os outros cientistas da época. Por isso, o primeiro a publicar a descrição do método acabou por ser um outro matemático, o francês Adrien-Marie Legendre (1752-1833), em 1805. Em 1809, Gauss publicou um livro no qual explicava em detalhe a sua previsão de 1801 (e não só), onde também afirmava que já tinha derivado o método dos mínimos desvios quadrados em 1795, 10 anos antes da publicação de Legendre.

Carl Friedrich Gauss (1777-1855), o príncipe da Matemática, considerado por muitos o maior matemático desde a antiguidade. Contribuiu de forma significativa em muitas áreas distintas da Matemática e da Física (álgebra, análise, estatística, geometria diferencial, teoria de números, mecânica, electrostática, astronomia, óptica, entre outras).

Repito que os dados pseudo-experimentais expostos neste artigo foram gerados com o seguinte código de MatLab criado por mim: least_squares; sinta-se à vontade para o explorar. Se desejar mais detalhes pode pedi-los nos comentários.

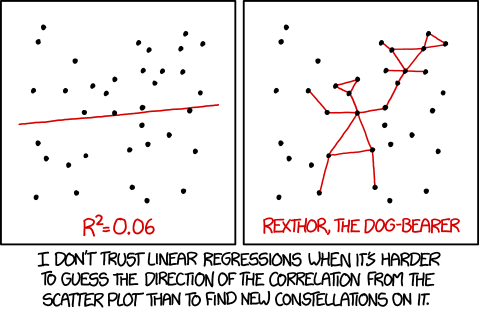
“Não confio em regressões lineares quando é mais difícil inferir a direcção de correlação dos pontos do que encontrar uma nova constelação neles.” Este sarcasmo visa criticar a imensidão de estudos que são publicados diariamente onde podemos encontrar regressões como a que vemos na imagem do lado esquerdo. Como é evidente, nestas condições a recta de ajuste não tem qualquer significado científico.