Soma dos naturais = infinito ou -1/12?

Qual a soma de todos os números naturais? Recordo que um número natural é um número inteiro maior que zero, isto é:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, …

Como deverá ser claro, este conjunto tem um número infinito de elementos. Mesmo o maior número natural que possam imaginar não será o “último” da lista, pois esse mesmo número +1 dá origem a um número maior, que também não será o “último” pela mesma razão (ad infinitum).

Talvez o leitor já tenha visto um famoso vídeo do Numberphile que afirma que a soma de todos os naturais é igual -1/12:

Será que é mesmo?
(Este artigo será um pouco denso, pelo que sinta-se à vontade de usar os comentários para pedir esclarecimentos adicionais. Acrescento que poderá ser útil ler primeiro o artigo 0.9(9)=1, onde faço a demonstração da soma da progressão geométrica.)

Antes de tentarmos calcular a soma de “todos”, comecemos por somar os primeiros 100 números naturais, um exercício famoso que alegadamente Carl Friedrich Gauss (1777-1855), o Príncipe da Matemática, terá resolvido quando tinha apenas 8 anos.

Permitam-me introduzir a notação de somatório, que me será útil ao longo deste artigo:

A letra grega ∑ denota somatório, e a expressão “traduz-se” na soma de k a começar em 1 até 100 (índices inferior e superior de ∑, respectivamente), tal como explicita o lado direito da equação.

Em vez de começarmos a somar os números sem pensar, reconheçamos antes o que Gauss constatou: o primeiro número mais o último (1+100) é igual ao segundo mais o penúltimo (2+99), e também ao terceiro mais o antepenúltimo (3+98)… Isto significa que podemos agrupar em pares todos os números da lista, e a soma de cada par é igual a 101. Quantos pares temos? Com 100 podemos fazer 50 pares. Portanto o resultado é 101 somado essas 50 vezes, ou seja:

Este resultado é fácil de generalizar para a soma dos primeiros N números naturais:

No caso anterior N era 100. Em geral, podemos sempre agrupar os N números em N/2 pares, cuja soma é (N+1). Se o leitor estiver preocupado com os números ímpares, repare que é fácil de provar que este resultado também é válido para números ímpares (ainda que neste caso N/2 não represente um número inteiro de pares). Para o provar, considere que N=2M+1 (em que M é 0 ou um número natural), o que garante que N seja ímpar. Substituindo na fórmula de cima:

Como 2M é par, a soma deste não oferece dúvidas:

Substituindo M por (N-1)/2, verificam que de facto:

Sabemos, portanto, qual o resultado de somar os N primeiros números naturais. Como é fácil de perceber, quanto maior for o N, maior é a soma. O gráfico abaixo representa a forma como a soma varia em função de N:

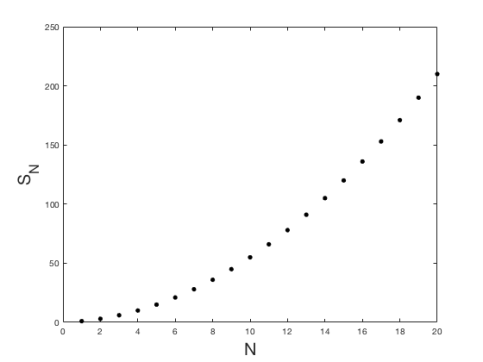
Como podem “adivinhar” (e provar), esta função é sempre crescente. Assim, quando N tende para infinito, a soma também tende para infinito.

Sendo assim, porque é que no vídeo afirmam que a soma de todos os números naturais é -1/12?

A “demonstração” apresentada no vídeo faz uso da seguinte soma infinita (série de Grandi):

Fazendo somas parciais, constatamos que se somarmos (por ordem) um número par de elementos, o resultado é zero, enquanto que se for um número ímpar obtemos 1. Não existe convergência: por mais elementos que adicionemos, o resultado será sempre 1 ou 0. A “demonstração” apresentada no vídeo mostra que esta soma é igual a 1/2, o que é portanto falso. Na verdade, usando séries ditas divergentes como esta, é possível de “demonstrar” qualquer tipo de paradoxo. Por exemplo, imagine-se que se somam duas séries destas:

A soma das duas séries é igual à própria série original, portanto 2S=S, o que é o mesmo que dizer que 2=1 se S for diferente de zero. Isto implica que S é zero? Não. S não está definido.

Recordando as palavras do matemático norueguês Niels Henrik Abel (1802-1829): “As séries divergentes são invenção do diabo, e é vergonhoso basear nelas qualquer tipo de demonstração.”

Não obstante, é possível atribuir números a séries infinitas, através, por exemplo, da soma de Cesàro, mas isso é outra história…

Mas os autores do vídeo são investigadores de Física e Matemática… Como é que é possível que eles não saibam isto?

De certo que sabem. No entanto, deram-se a liberdades excessivas com o intuito de simplificar e aumentar o impacto do vídeo. Para tal, sacrificaram o rigor científico.

Então isso implica que o -1/12 sempre tem algum sentido?

Sim. Para lá chegarmos, consideremos primeiro a seguinte soma:

Trata-se da soma dos inversos dos quadrados dos números naturais. Esta soma não diverge, isto é, a soma de todos os elementos tende para um número: π²/6. A demonstração não é muito difícil para quem tem alguma prática, mas é demasiado extensa para a apresentar aqui (se tiver interesse, poderá consultá-la aqui). A demonstração foi feita pelo grande matemático suíço Leonhard Euler (1707-1783). Esta soma é particularmente famosa por o resultado ser função da constante π. A Matemática tem muitas vezes o dom de nos surpreender com as relações que se criam entre áreas diversas. Neste caso, não é de todo evidente por que razão o quociente entre o perímetro e o diâmetro de qualquer círculo tenha algo a ver com a soma infinita dos inversos dos quadrados dos números naturais.

A série de cima pode ser generalizada se substituirmos o quadrado por uma variável s:

Esta é a função zeta de Euler. Pode-se demonstrar que esta função converge se s>1, isto é, a soma de todos os termos tende para um valor finito, tal como se viu no caso s=2, em que o valor é π²/6. Para s=1 temos a série harmónica cuja divergência é habitualmente estudada em cadeiras de Matemática do primeiro ano universitário (de cursos de ciências exactas); se tiver interesse, pode consultar as demonstrações clássicas presentes na wikipedia.

s pode não só ser real, como podemos assumi-lo como sendo um número complexo. Nesse caso a função toma o nome de função zeta de Riemann (ou Euler-Riemann), da qual já vos falei um pouco no artigo sobre os Problemas do Milénio. Isto de generalizar para o plano complexo é chamado de continuação analítica em análise complexa. Trata-se de uma técnica bastante útil para estudar certas funções. É importante frisar que a função zeta de Riemann só coincide com a função de Euler para s real e maior que 1! De facto, para s=-1, a função zeta de Riemann é igual a -1/12 (a demonstração é demasiado complexa para a expor aqui), enquanto que a de Euler diverge.

A título de curiosidade, e tal como houvera referido no artigo dos Problemas do Milénio, acrescento que um dos interesses principais da função zeta de Riemann concerne a sua relação com os números primos. Essa relação foi descoberta também por Euler, que demonstrou a seguinte igualdade:

onde ∏ é o símbolo de produtório (similar ao ∑), e “primos p” significa que os produtos se estendem por todos os números primos (que são infinitos, como provei neste artigo, seguindo a demonstração de Euclides). Ou seja:

A demonstração é engenhosa, mas muito simples! Se compreendeu a demonstração para uma progressão geométrica (que ilustrei no artigo 0.9(9)=1), então ser-lhe-á fácil de perceber também esta (veja-a na wikipedia). Pode-se ainda constatar que a partir desta fórmula obtemos uma nova demonstração de que os números primos têm que ser infinitos, caso analisemos s=1, visto que a soma do lado esquerdo corresponde à série harmónica, a qual diverge. Fica o desafio de fazer esta demonstração.

“Sabias que a soma de todos os inteiros positivos é -1/12?”
“A sério? Portanto, tecnicamente, se me emprestares dinheiro sem fim, acabas por ser tu a ficar-me a dever dinheiro?”
“Bom, estás a tomar isto demasiado literalmente.”
“Estou a começar a apaixonar-me pela Matemática!”