Como equilibrar uma mesa com Matemática?

Já lhe aconteceu ir ao café, pedir a sua bebida, e constatar que a mesa junto à qual está sentado não está bem assente com as quatro pernas no chão? Ao apoiar um cotovelo na mesa, esta baloiça, colocando em risco a sua bebida! Se você for como eu, irá de certo decidir que tal contratempo é inaceitável! Como é que resolve o problema? Olha em redor e encontra um jornal esquecido na mesa ao lado… Retira-lhe os inúteis classificados, e faz com eles uma almofada para colocar debaixo de uma das pernas da mesa (como a foto de cima ilustra). Problema resolvido! Já pode deleitar-se com a sua bebida em paz. Mas… E se não encontrar nenhum jornal? Se não tiver nada para colocar debaixo de uma das pernas? Fácil: rode a mesa em torno do seu centro até esta ficar estável! A Matemática garante que existirá pelo menos um ponto de estabilidade!

Para não ser acusado de ser mentiroso, primeiro devo referir as condições para que a afirmação de cima seja de facto verdadeira. Por um lado é necessário que as pernas tenham todas o mesmo comprimento, pois, como é fácil de imaginar, se uma das pernas tiver, por exemplo, metade do comprimento das outras, é óbvio que por mais que se rode a mesa nunca a iremos conseguir estabilizar. Desta condição pode-se deduzir que a imperfeição tem que estar no chão. Não obstante, o chão também tem que obedecer a uma condição: tem que ser uma superfície contínua, sem buracos. Ainda em relação à mesa, as pernas têm que formar um quadrado ou um rectângulo, uma condição que se verifica para grande parte das mesas.

Na prática não existem mesas perfeitas, nem superfícies completamente lisas, porém o resultado matemático é ainda assim em geral aplicável. Convido-o, por isso, a experimentar a rodar a mesa da próxima vez que se defrontar com uma mesa instável.

Este resultado matemático é conhecido como o Teorema da Mesa Bamboleante (tradução livre de The Wobbly Table Theorem), cujo argumento empírico foi apresentado em 1973 na Scientific American pelo muito conhecido divulgador de Matemática americano, Martin Gardner (1914-2010). Só muito recentemente, em 2005, o teorema foi de facto demonstrado pelo matemático Burkard Polster. Este teorema é uma consequência do Teorema do Valor Intermédio, que passarei a apresentar com um exemplo.

Consideremos que o gráfico seguinte representa a posição de um atleta (preguiçoso) em função do tempo:

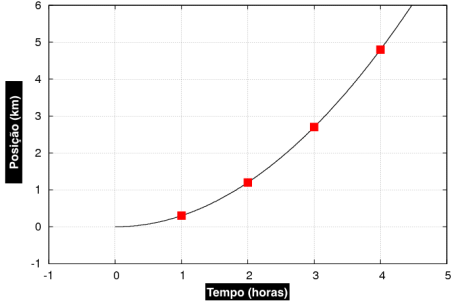
Podemos convencionar que a posição zero corresponde a um dado ponto de partida, e que as subsequentes posições correspondem às distâncias em relação a esse ponto. O gráfico mostra que à medida que o tempo passa, o atleta afasta-se do ponto de partida, e que o faz cada vez mais depressa, isto é, a sua velocidade está a aumentar. (Se tiver questões sobre a interpretação do gráfico, não se coíba de as colocar nos comentários.)

Antes de apresentar o teorema, devo ainda esclarecer o que se entende por “continuidade”: o gráfico de cima é contínuo porque a posição em função do tempo segue uma curva ininterrupta. Uma descontinuidade corresponderia a um “salto” no gráfico, isto é, de um momento para o seguinte, a posição teria uma variação brusca. Por outras palavras, quaisquer dois tempos quase consecutivos correspondem sempre a duas posições muito próximas.

O Teorema do Valor Intermédio afirma algo muito intuitivo: como a posição em função do tempo é contínua, a posição do atleta começa em zero, e ao fim de 4h está nos 4.8 km, então é garantido que o atleta passou por qualquer posição entre os 0 e 4.8 km a uma dada altura nessas quatro horas. Note-se que esta afirmação é sempre verdadeira para qualquer gráfico da posição em função do tempo, contando que se verifique a continuidade. Pode imaginar que por mais voltas que o atleta dê, se num dado momento (i) ele se encontra na posição A, e num momento posterior (ii) está numa posição B, então ele terá que ter passado por qualquer das posições entre A e B pelo menos num dado momento entre (i) e (ii) (em certas posições pode ter passado mais que uma vez).

Acrescento ainda que o Teorema do valor intermédio é uma versão mais geral do Teorema de Bolzano, no qual uma função contínua que tem um ponto negativo e um ponto positivo, terá que necessariamente intersectar o zero:

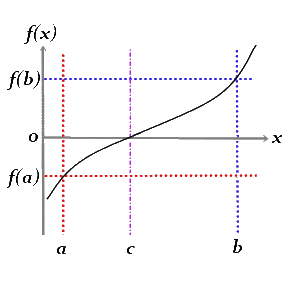
Munidos deste teorema estamos em condições de compreender o Teorema da Mesa Bamboleante. Inicialmente a mesa tem duas pernas estáveis, em cantos opostos, e pode oscilar devido ao facto das duas outras pernas não tocarem o chão em simultâneo. Considere que a mesa é quadrada, para simplificar, ainda que, como disse, pudesse ser rectangular. Podemos então pressionar a mesa num dos cantos oscilantes, de forma a que fique com três pernas assentes no chão, e uma no ar. Note que podemos fazer rodar a mesa mantendo sempre essas mesmas três pernas assentes no chão, mantendo a pressão sempre sobre a mesma perna. À medida que rodamos a mesa, a distância entre a perna no ar e o chão varia de forma contínua, dado o chão ser uma superfície contínua. É aqui crucial reconhecer que não é possível continuar a rodar até completar um quarto de volta (90 graus), pois essa posição é equivalente à inicial. Estaríamos a tentar fazer com que a “perna no ar” chegasse à posição que antes era “estável”, mantendo as outras três pernas assentes no chão. Se tal não era possível inicialmente, depois de rodar a mesa 90º também não será (visto todas as pernas terem o mesmo comprimento). Para fazer essa rotação de 90º estar-se-ia a forçar a “perna no ar” a “furar” o chão! Isto implica, portanto, que existe pelo menos um ponto intermédio nessa rotação de 90 graus onde a perna que estava no ar encontra o solo, permitindo estabilizar a mesa.

Convém talvez adicionar que a posição de estabilidade não corresponde necessariamente a uma mesa bem nivelada. Terá, por isso, que ter cuidado para que a sua bebida não deslize e caia no chão.

“Só em problemas de Matemática é que podemos comprar 60 meloas e ninguém nos perguntar se não estamos bem da cabeça.”
Este cartoon ilustra um problema que eu atribuo a professores preguiçosos e irresponsáveis, que não se dão ao trabalho de inventar questões realistas, e que com isso promovem a ideia errónea de que a Matemática é uma disciplina distante da realidade de todos os dias.