Erros e mal-entendidos

No final do ano é comum fazer-se uma análise do que se passou nos últimos 12 meses para se planear o que fazer no próximo ano. Uma forma útil de condensar a informação é reduzi-la a números. Por exemplo, como foi a natalidade em 2021? E a mortalidade? Acidentes na estrada? Criminalidade? Para que estes números tenham algum significado prático convém compará-los aos dos anos anteriores. No caso da criminalidade, desejar-se-á que esteja a diminuir. Infelizmente, a análise que se vê nos noticiários tende a parar neste ponto: se diminuiu é óptimo; se aumentou é dramático. O que aqui falta é o avaliar do quão óptima ou dramática é a diferença nos números. Ou se a diferença é tão reduzida que não faça sentido ficar-se satisfeito ou insatisfeito com as mudanças relativas. Pior ainda, em certos casos os dados são-nos apresentados sob a forma de gráficos adulterados, cuja interpretação precisa de ser bastante cuidadosa.

Consideremos o gráfico abaixo:

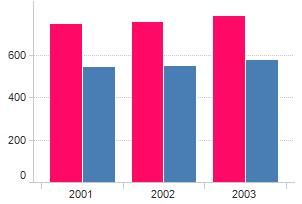
O gráfico pretende ilustrar as rendas mensais de T0s e T1s ao longo dos anos de 2001, 2002 e 2003. A primeira coisa a constatar é que as barras devem representar valores médios de renda (isto é, a altura da barra representa a renda média). Apartamentos diferentes terão rendas diferentes. O valor médio consiste em calcular a soma de todos os valores de renda apurados e dividir pelo número de apartamentos em causa (para cada tipologia e para cada ano de forma separada). O que constatamos de seguida é que este valor médio pode ter pouco significado só por si. A variabilidade de rendas pode ser imensa e olhando só para a média não é possível avaliar essa variabilidade. Para representar esta variabilidade podem-se acrescentar barras de erro ao gráfico:

Uma barra de erro pode ser definida como a média dos desvios em relação à média. Por exemplo, se tivéssemos três apartamentos com rendas de 500, 550 e 600€ por mês, a média seria (500+550+600)/3 = 550€, enquanto que os desvios em relação à média de cada apartamento seriam, respectivamente, de 500-550 = -50€, 550-550 = 0€, e 600-550€ = 50€. Na consideração dos desvios negligenciamos se são negativos, pelo que o desvio médio seria (50+0+50)/3 = 33€. (Há outras definições de desvios que podem ser mais apropriadas em certas circunstâncias.) A barra a colocar no gráfico teria a altura correspondente a 2 vezes os 33€, centrada na média, de forma a representar possíveis desvios de 33€ tanto acima da média, como abaixo.

Qual a importância destas barras de erro? De acordo com a figura, com elas podemos ter mais certezas sobre a generalidade de os T1s terem sido mais caros que os T0s em 2001. Já em 2002, os T0s tiveram uma imensa variabilidade de rendas, pelo que seria possível encontrar muitos T0s com renda superior aos T1s. Isto é, a média das rendas dos T0s em 2002 parece ser um indicador muito redutor, em particular quando se queira comparar as rendas dos T0s com as dos T1s. Finalmente, só com as médias poder-se-ia pensar que as rendas tanto de T0s como de T1s aumentaram de 2001 para 2003. Contudo, quando consideramos os desvios compreendemos que provavelmente muitos apartamentos podem ter-se mantido mais ou menos com a mesma renda. Por outras palavras, não é claro que a diferença de rendas tenha mudado de forma significativa no mercado imobiliário entre esses anos. A diferença na média parece ser apenas uma oscilação insignificante na média.

Estas minhas interpretações dos desvios podem parecer um pouco subjectivas, mas esclareço que há técnicas estatísticas para que se possam tirar conclusões mais rigorosas.

Como é claro, a necessidade de barras de erro (ou de outros indicadores de variabilidade) são cruciais na interpretação de muitos outros números com que somos bombardeados diariamente. Por exemplo, durante a actual pandemia vai-se ouvindo de forma recorrente sobre os números de novos infectados e de mortos, dizendo-se o quanto estes vão diminuindo ou aumentando em relação ao dia anterior. Será que um aumento de 100 novos infectados diários é um aumento assustador, ou nem por isso? Para responder precisamos de saber o quanto é que os números costumam flutuar de dia para dia (desvios médios), assim como se há uma tendência de aumento, ou não.

Para além de ser comum serem-nos apresentados gráficos sem barras de erro, temos ainda que ter o cuidado de verificar se o gráfico mostra de facto aquilo que pensamos que estamos a ver. Por exemplo, consideremos o gráfico abaixo:

Nota alguma diferença em relação ao gráfico inicial? Assumindo que as barras indiquem o mesmo, à primeira vista parece que as rendas dos T1s (barras vermelhas) são praticamente o dobro das rendas dos T0s (barras azuis). Porém, os valores indicados na barra vertical do lado esquerdo são os mesmos que aqueles que apareciam nas figuras de cima. O gráfico em si não está errado, mas foi alterado de tal forma que pode induzir em erro. Neste caso as barras não começam do zero, pelo que as diferenças relativas de altura entre barras foram como que inflacionadas visualmente. Da próxima vez que lhe for apresentado um gráfico no noticiário tenha o cuidado de se certificar que a altura das barras corresponde às suas expectativas.

Uma outra manipulação possível seria a remoção de alguns anos do eixo horizontal. Por exemplo, se o gráfico representasse a evolução das rendas nos últimos 20 anos, seria importante verificar que não havia anos em falta. Pode-se imaginar que um agente imobiliário poderia ter interesse em demonstrar que o mercado tinha estado sempre a aumentar nos últimos anos, pelo que poderia omitir do seu gráfico alguns anos em que o mercado estivera estagnado.

Não obstante, nem todas as manipulações gráficas têm que induzir em erro ou ter propósitos desonestos. Em certas circunstâncias pode de facto ser útil omitir informação redundante para tornar mais clara uma dada mensagem que se pretenda transmitir.

TED lesson que serviu em parte de inspiração para este texto: How to spot a misleading graph.