Há uns anos atrás, quando aprendi as dízimas infinitas periódicas e me disseram que são números racionais, comecei a questionar-me:
“Humm… Existe o teorema que diz que entre dois números racionais existe sempre um número irracional! Nesse caso, entre 0.9(9) e 1, que número existe? Como pode ele existir?”
A verdade é que não existe, porque eles são um só número, apenas representados de forma diferente.
Uma forma simples de constatar isto é pensar:
Se multiplicarmos por 3 dos dois “lados”…
Como vêem, trata-se do mesmo número, mas “disfarçado”.
É possível demonstrar de uma forma mais elegante, usando a soma de uma série infinita:
Nesta demonstração usei o seguinte facto (progressão geométrica):
Isto é muito fácil de demonstrar. Primeiro deixem-me explicitar o que significa o somatório (a letra grega sigma maiúscula):
Notem que se o módulo de r não for inferior a 1, esta soma dá infinito. Pode-se seguidamente fazer o seguinte “truque”:
Logo:
Portanto:
E finalmente:
O “truque” em causa permite-vos demonstrar muitos resultados de somas de séries.




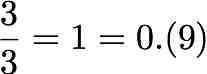
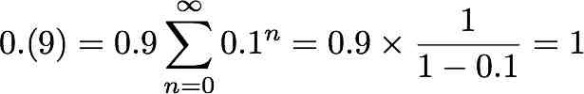
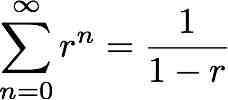
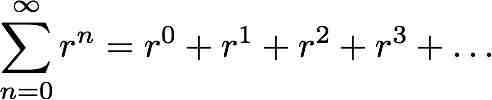
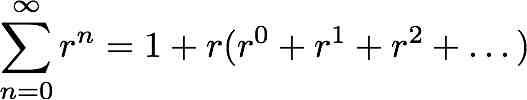
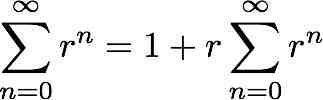
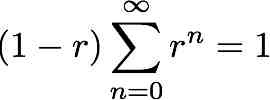


2 comentários
2 pings
Acho que não há irracionais entre 0,(9) e 1 porque não se consegue escrever o 0,(9) como a razão entre dois inteiros diferentes.
Author
Que é o mesmo que dizer que 0,(9)=1, visto que a razão entre dois inteiros iguais é 1. 🙂
[…] para pedir esclarecimentos adicionais. Acrescento que poderá ser útil ler primeiro o artigo 0.9(9)=1, onde faço a demonstração da soma da progressão […]
[…] porém, que o frigorífico é “alcançado no infinito”. Recorde o artigo em que provei que 0.9(9)=1. A soma da série infinita ½ +¼+1/8+… é equivalente à última fórmula presente nesse […]