O Extraordinário Pêndulo de Foucault – Parte I

O pêndulo de Foucault é uma daquelas experiências simples que têm o dom de explicar e quantificar algo que parece que as transcende. Esta experiência ilustra bem o poder da Física e a forma como fenómenos aparentemente distintos podem estar relacionados.

O leitor conhece o fio de prumo da construção civil? Como o nome indica, é um fio que serve para verificar a verticalidade de algo (de uma parede, por exemplo):

O fio tem um peso na ponta que permite ao fio ficar bem esticado, indicando a direcção vertical (devido à força gravítica). Este fio de prumo transforma-se num pêndulo se soltarmos o peso de uma posição que não a de repouso (com o fio esticado). O peso oscila em torno da posição de equilíbrio (a de repouso):

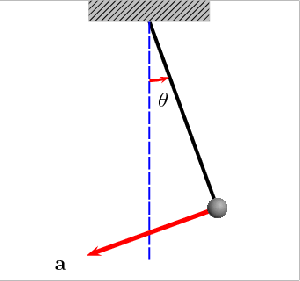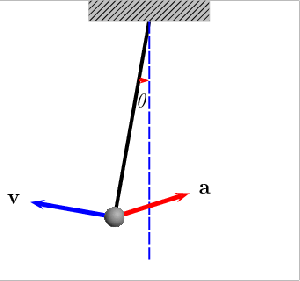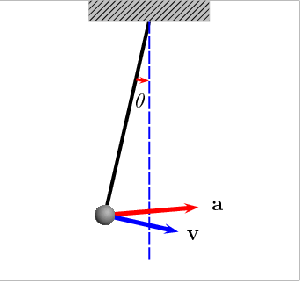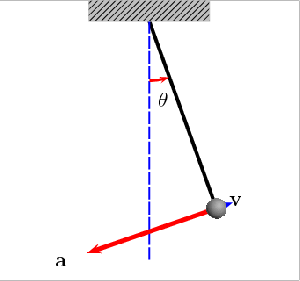
Na imagem, a linha azul a tracejado indica a direcção vertical; a letra grega θ é o ângulo que o fio faz com a vertical (o ângulo máximo corresponde ao ângulo do qual se largou o peso, que aqui é representado pela esfera cinzenta); o rectângulo superior representa uma “plataforma” fixa pela qual o fio está suspenso; a seta vermelha (vector) assinala a direcção, sentido e magnitude da aceleração ‘a’ (que coincide com a força aplicada na esfera); e o vector azul ‘v’ corresponde à velocidade da esfera. Notem que o vector velocidade “desaparece” nos pontos de maior amplitude, porque o pêndulo pára antes de voltar no sentido contrário; por outro lado, a força tem direcção vertical no ponto de equilíbrio, porque a esfera só sente duas forças: a gravítica que tem sempre direcção vertical, e a força do fio, que impede que o fio caia (se o leitor não estiver muito familiarizado sobre o conceito de força em Física, poderei responder a dúvidas em comentário). Neste caso não existe qualquer resistência (amortecimento), pelo que o pêndulo mantém inalterável as suas oscilações. Se existisse resistência do ar, por exemplo, a amplitude das oscilações iria diminuir gradualmente, até que o pêndulo acabaria por parar na posição de equilíbrio. A amplitude nunca pode aumentar, porque isso violaria o princípio da conservação da energia:

 No vídeo é referido que a energia total do sistema mantém-se: a energia potencial (devido à gravidade) aumenta com a altura, enquanto que a energia cinética (devido ao movimento) aumenta com a velocidade (estas duas energias estão relacionadas com as setas indicadas na imagem de cima). O apresentador ainda acrescenta que se for dada energia à bola, então sim, esta já consegue ultrapassar a posição inicial. Tal como no baloiço, ao acrescentar energia ao movimento através do “empurrão”, o movimento de oscilação ganha amplitude.

Quando um pêndulo oscila com amplitude constante, tem um período de oscilação constante, como é evidente (o período é igual ao tempo que demora a oscilação a repetir-se, ou seja, corresponde ao tempo que o pêndulo leva a voltar a uma das posições extremas, de maior amplitude, da oscilação; as posições intermédias são “atravessadas” duas vezes por período). Esta característica foi usada para se criarem relógios, visto que estes precisam apenas de um mecanismo interno que marque a passagem do tempo de forma regular. A partir do período do pêndulo, basta definir a nossa convenção de “divisão temporal”, para traduzir um dado número de períodos num determinado tempo. A maioria dos relógios de pêndulo são feitos de modo a que um período do pêndulo coincida com a nossa convenção de 1 segundo.

 Galileu foi o primeiro a estudar a forma como poderia ser feito um relógio de pêndulo, porém, o primeiro exemplar só apareceu em 1656, desenhado por Christiaan Huygens.

 O relógio de pêndulo manteve-se como o mais preciso até à década de 1930, quando surgiu o relógio de quartzo, baseado na frequência de ressonância de um material piezoeléctrico (como referido no artigo sobre o rádio). Naturalmente, o problema do relógio de pêndulo está na dificuldade em manter o período constante, uma vez que, como disse em cima, os pêndulos tendem a parar devido a forças de atrito (resistência ao movimento). Os relógios de pêndulo que o leitor deverá conhecer implicam que se “puxe a corda”, por exemplo, que corresponde a um mecanismo que serve para compensar as forças de atrito, de forma a manter o período constante. Contudo, o mecanismo não é perfeito: o seu grau de perfeição define a precisão do relógio (entre outros detalhes).

Voltemos então ao pêndulo de Foucault. Que tem de especial este pêndulo? Nada, excepto o seu tamanho. O pêndulo que Foucault criou em 1851 tinha um “fio” de 67 metro e um peso de 28 quilograma.

 Pêndulo de Foucault no Panteão de Paris (este pêndulo é na verdade uma cópia do original).

Em cima, quando descrevi o movimento do pêndulo, deixei implícito que a linha do pêndulo atravessava sempre o mesmo plano vertical. Por outras palavras, se colocassem o pêndulo a oscilar paralelamente a uma parede, o peso nunca iria tocar na parede, assumindo que o fio tinha partido de uma posição inicial paralela à parede. De facto, se o pêndulo tiver a liberdade de oscilar em qualquer plano vertical (algo que não acontece no caso do relógio de pêndulo, em que um só plano é permitido), o peso irá mesmo bater na parede, se esta estiver suficientemente próxima. Foucault fez um pêndulo enorme exactamente para que o fenómeno fosse facilmente visível (e mensurável).

Mas de onde vem esta rotação do plano de oscilação?

A rotação da Terra é a responsável! Analisando a velocidade com que o plano de oscilação roda é possível estimar a latitude em que o pêndulo está instalado! O como e o porquê serão questões para a segunda parte deste artigo.

 Tradução: “Estás a ficar com sono, com muito soooono… Aaargh! Nunca consigo meter esta coisa estúpida a balançar!”

Mais um falhanço no hipnotismo submarino.